K-Means算法实现

本篇博客的主要内容有：

K-means算法
python代码实现
- 任意选择K(类别)聚类
- 选取最佳的k,画出聚类后的图像分布
- 计算准则函数J,画出J的变化图像
- 完整python代码

试用K—均值法对如下模式分布进行聚类分析。编程实现，编程语言不限。
{x1(0, 0), x2(3,8), x3(2,2), x4(1,1),
x5(5,3), x6(4,8), x7(6,3), x8(5,4),
x9(6,4), x10(7,5)}

K-Means算法

K均值是一种动态巨累法
动态聚类法先粗略地进行预分类，然后再逐步调整，直到把类分得比较合理为止，这种方法计算量较小、使用内存量小、方法简单,适用于大样本的聚类分析。
K均值算法的思想是首先任意选取K个聚类中心，按最小距离原则将各模式分配到K类的某一类,再不断计算聚类中心和调整各模式的类别,最终使各模式到其判属类别中心的距离平方之和最小。
具体步骤:

任意选K个聚类中心(可以随机,或者直接选样本的前K个,后面会动态调整)
遍历所有样本,将每个样本按照最小距离原则分到K类中的一类
更新聚类中心,具体为将每个类别的聚类中心改为该类中所有样本的均值
一直重复上述过程,直到聚类中心保持不变。

这里有个问题是,为什么聚类中心为什么要选择样本的均值,在下面的准则函数中将会给出推导过程。
所以K均值算法的实现最重要的就是计算距离和均值。

准则函数定义

对于第j个类别$S_{j}$,有$N_{j}$个样本,聚类中心为$Z_{j}$

$J_{j} = \sum_{i=1}^{N_{j}}\parallel X_{i} - Z{j} \parallel ^{2}$

(这里应该是二范数的平方,markdown公式和博客代码不是很兼容的原因导致只是显示了一条竖线)
对于所有K个类别的准则函数就是把每个类别的求和就行

由上面的准则函数,可以得到,对于某一个聚类$j$,应有:

$\frac{\partial J_{j}}{\partial Z_{j}} = 0$

那么有:

$\frac{\partial \sum_{i=1}^{N_{j}}\parallel X_{i} - Z{j} \parallel ^{2}}{\partial Z_{j}} = \frac{\partial \sum_{i=1}^{N_{j}}(X_{i}-Z_{j})^{T}(X_{i}-Z_{j}) }{\partial Z_{j}} = 0$

可以解得:
$Z_{j}= \frac{1}{N_{j}}\sum_{i=1}^{N_{j}}X_{i},X_{i} \in S_{j}$

所以为了使得准则函数最小,$S_{j}$类的聚类中心应选为该类样本的均值

下面是作业的python实现。

K-Means的python实现

首先,K均值算法的K我们是没有办法事先预知的,所以,我先画出了图像的分布情况。
下面是原始数据,将其保存在txt文件中:
1
2
3
4
5
6
7
8
9
10
0,0
3,8
2,2
1,1
5,3
4,8
6,3
5,4
6,4
7,5
先将其读入,并且画出图像
1
2
path = 'data.txt'
data = pd.read_csv(path, header=None, names=['x1', 'x2'])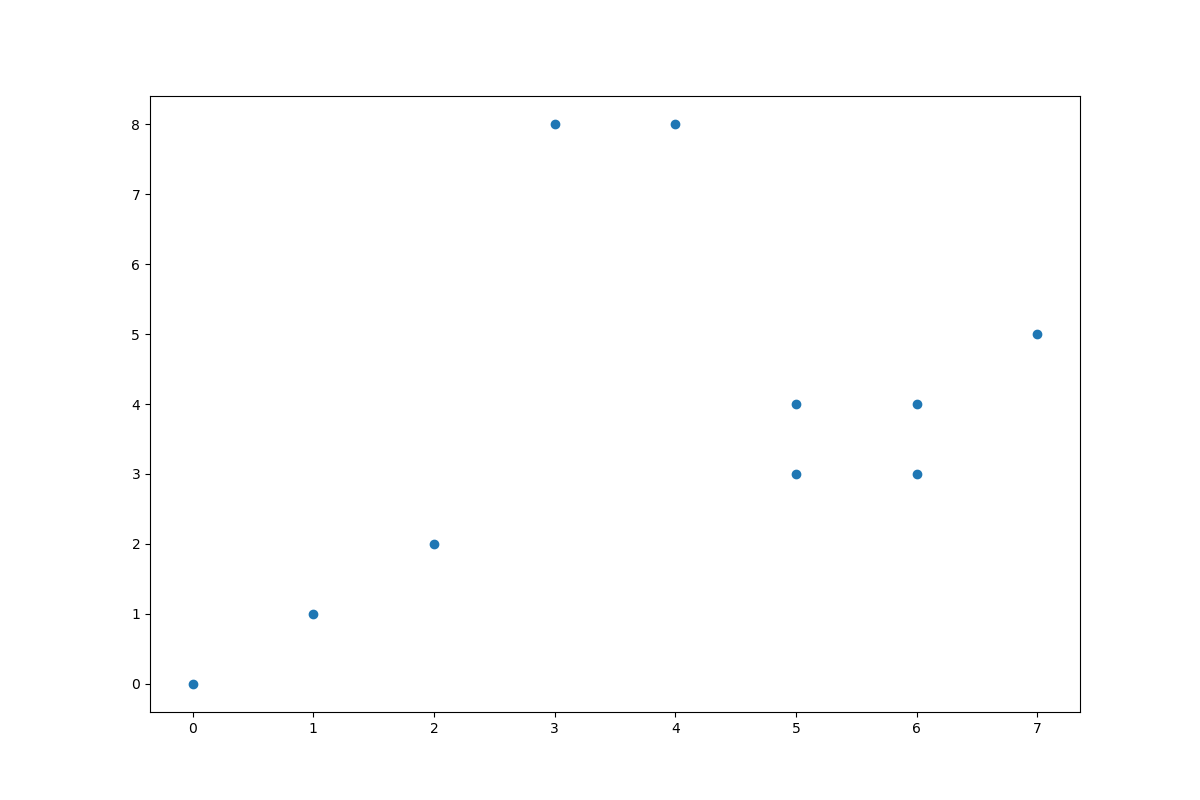
计算距离
1
2
def calDist(X,center):
return np.linalg.norm(X - center,2,1)
这里直接返回了二范数的距离(平方再开根号)

K-means算法的实现

def kmeans(X,k):
#@ return centers,clusters[每个聚类中心,每个样本所属的类别]
    centers = X[:k,:]
    newCenters = np.zeros(centers.shape)
    clusters = np.zeros(len(X))
    while True: #当聚类中心不再变化时算法停止

        #计算每个点到所有中心的距离
        for i in range(len(X)):
            d = calDist(X[i], centers)
            cluster = np.argmin(d) 
            clusters[i] = cluster #第i个样本的类别设定为到所有聚类中心最近的那个
        #遍历k个中心,分别找出以该聚类中心的所有点并且求均值作为新的聚类中心
        for i in range(k):
            points = [X[j] for j in range(len(X)) if clusters[j] == i]
            newCenters[i] = np.mean(points, axis=0)
        if (centers == newCenters).all():#当聚类中心不再变化时,终止循环
            break 
        else:
            centers = newCenters
    return centers,clusters

K = 3的代码分析

由于我们之前已经画出了图像,可以很自然的得到他应该分为3个类别,使用K-means算法,并画出图像

centers,clusters = kmeans(X,k)
colors = ['r', 'g', 'b']
fig, ax = plt.subplots()
for i in range(k):
    points = np.array([X[j] for j in range(len(X)) if clusters[j] == i])
    #上面是3*1*2的array,先用flatten变为1*len(X)维的,再reshape
    points = points.flatten()
    points = np.reshape(points,(int(len(points)/2),2))
    print(points[:,0],points[:,1])      
    ax.scatter(points[:,0],points[:,1], s=20, c=colors[i])
ax.scatter(newCenters[:, 0], newCenters[:, 1], marker='*', s=30, c='y')
plt.show()

下面是K-means算法后的结果,其中五角星是聚类中心

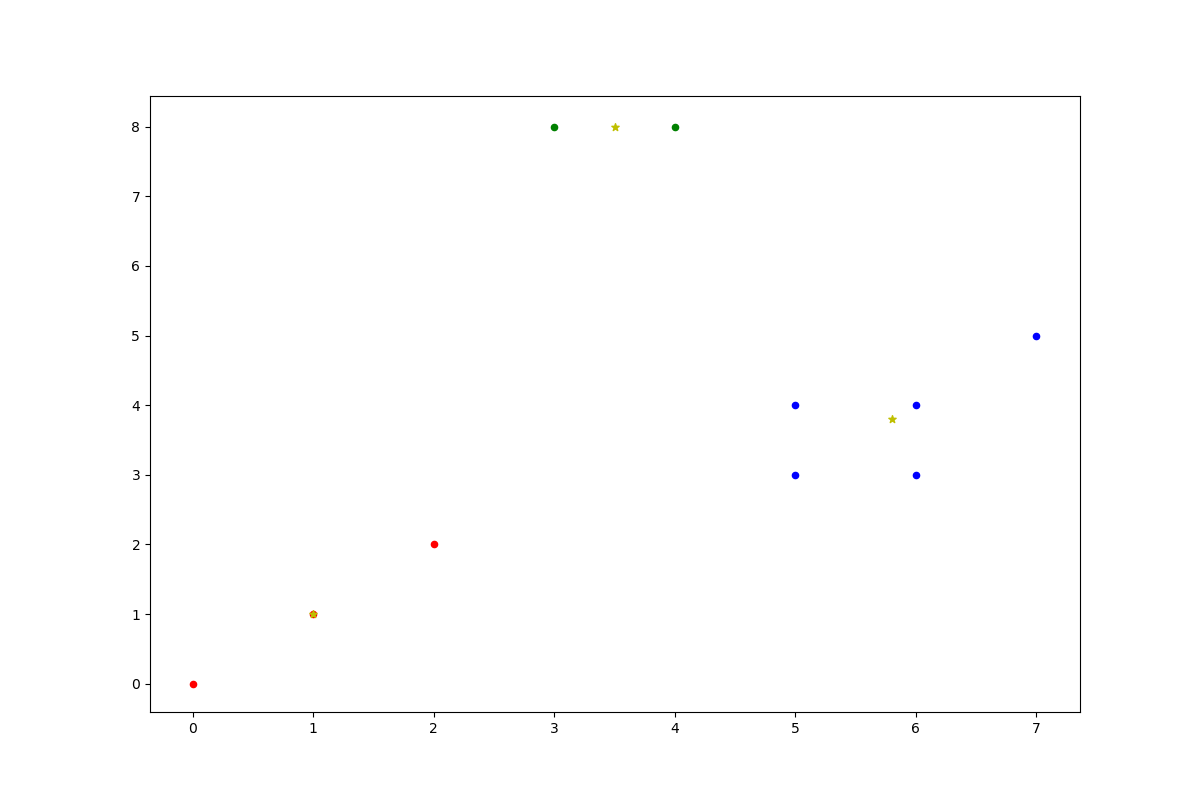
由图可知,分成了三类,每个聚类中心分别为

1
2
3

[[1.  1. ] 
 [3.5 8. ] 
 [5.8 3.8]]

取K不同值时J的变化


J = np.zeros([11,1])
with warnings.catch_warnings():
    warnings.filterwarnings('error')
    #依次计算出J[k](准则函数)
    for k in range(1,11):
        try:
            centers,clusters = kmeans(X,k)
            for i in range(len(X)):
                d = calDist(X[i],centers[int(clusters[i])])
                J[k] = J[k] + (d**2)              
        except:
            print("None")
            
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(range(1,11), J[1:], 'b')

#下面是为了标出每个点的坐标
for i_x, i_y in zip(range(1,11), J[1:]):
    plt.text(i_x, i_y, '({}, {})'.format(i_x, i_y))
ax.scatter(range(1,11),J[1:])
ax.scatter(3,J[3:],'r')
ax.set_xlabel('k')
ax.set_ylabel('J')
ax.set_title('J vs k')
plt.show()

下面是取不同k值的j的变化.这里的J是距离平方的和

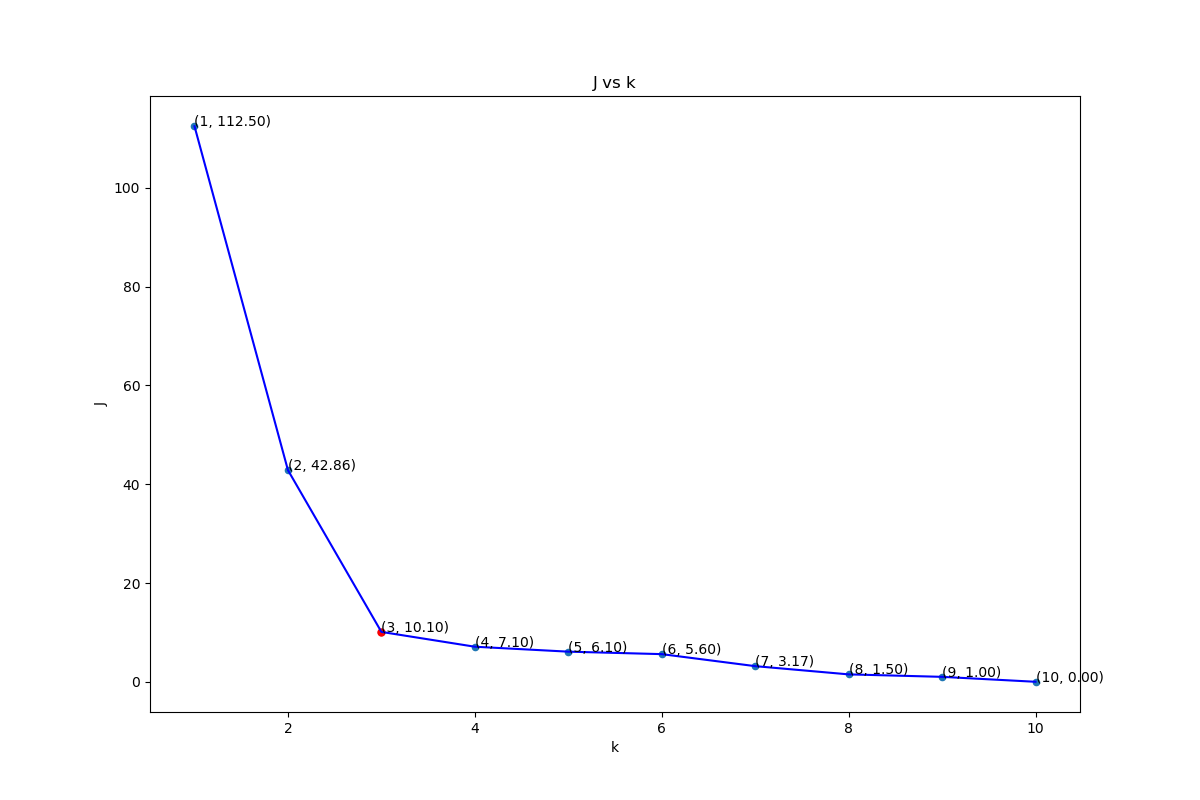
一般来说,如果样本集的合理聚类数为K类，当类别数从1增加到K时准则函数迅速减小，当类别数超过K时，准则函数虽然继续减少但会呈现平缓趋势。所以K一般会选择在拐点
上图中K=3的时候是比较合适的点(在K>3之后下降缓慢)。

K均值的结果受到所选聚类中心的个数和其初始位置的影响较大,实际应用中需要试探不同的K值和选择不同的聚类中心起始值。(这里我直接取了前K个样本)

完整代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings

def calDist(X,center):
    return np.linalg.norm(X - center,2,1)

def kmeans(X,k):
    np.seterr(invalid='ignore')
    centers = X[:k,:]
    newCenters = np.zeros(centers.shape)
    clusters = np.zeros(len(X))
    while True:
        for i in range(len(X)):
            d = calDist(X[i], centers)
            cluster = np.argmin(d) 
            clusters[i] = cluster
        for i in range(k):
            points = [X[j] for j in range(len(X)) if clusters[j] == i]
            newCenters[i] = np.mean(points, axis=0)
        if (centers == newCenters).all():
            break 
        else:
            centers = newCenters
    return centers,clusters

def plotPoints(X,centers,clusters,k):
    colors = ['r', 'g', 'b', 'y', 'c', 'm']
    fig, ax = plt.subplots()
    for i in range(k):
        points = np.array([X[j] for j in range(len(X)) if clusters[j] == i])
        points = points.flatten()
        points = np.reshape(points,(int(len(points)/2),2))
        print(points[:,0],points[:,1])      
        ax.scatter(points[:,0],points[:,1], s=7, c=colors[i])
    ax.scatter(centers[:, 0], centers[:, 1], marker='*', s=10, c='y')
    plt.show()

def main():
    path =  'data.txt'
    data = pd.read_csv(path, header=None, names=['x1', 'x2'])
    X = data
    X = np.matrix(X.values)
    J = np.zeros([11,1])
    with warnings.catch_warnings():
        warnings.filterwarnings('error')
        for k in range(1,11):
            try:
                centers,clusters = kmeans(X,k)
                for i in range(len(X)):
                    d = calDist(X[i],centers[int(clusters[i])])
                    J[k] = J[k] + (d**2)              
            except:
                print("None")      
    fig, ax = plt.subplots(figsize=(12,8))
    ax.plot(range(1,11), J[1:], 'b')
    # ax.scatter(3,J[3],'r')
    for i_x, i_y in zip(range(1,11), J[1:]):
        plt.text(i_x, i_y, '({}, {})'.format(i_x, i_y[0]))
    ax.scatter(range(1,11),J[1:])
    ax.set_xlabel('k')
    ax.set_ylabel('J')
    ax.set_title('J vs k')
    plt.show()
main()

References

K-Means算法的Python实现
模式识别课的PPT