NG机器学习EX1(线性回归)

发表于 | 分类于 | | 热度: ℃
字数统计: 2.4k字 | 阅读时长 ≈ 10分钟

本篇博客的主要内容有：

  1. python实现的ex1
  2. 梯度下降
    • 特征缩放
    • 学习率选取
  3. 正规方程

这篇博客的主要来源是吴恩达老师的机器学习第一周、第二周的学习课程。其中部分内容参考自黄海广博士的笔记内容,先根据作业完成了matlab代码,并且学习将它用python来实现(博客中无matlab实现)。在学习的过程中我结合吴恩达老师的上课内容和matlab代码修改了一部分代码(个人认为有点小错误以及可以优化的地方)。

读入数据并且可视化数据

第一部分的数据由两列组成,第一列是population(城市人口),第二列是profit(食物车的利润),在这里是2D数据,我们可以可视化它。

  1. 读入数据
    1
    2
    3
    path =  'ex1data1.txt'
    data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
    data.head()
  2. 画出数据的分布
    1
    2
    data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8))
    plt.show()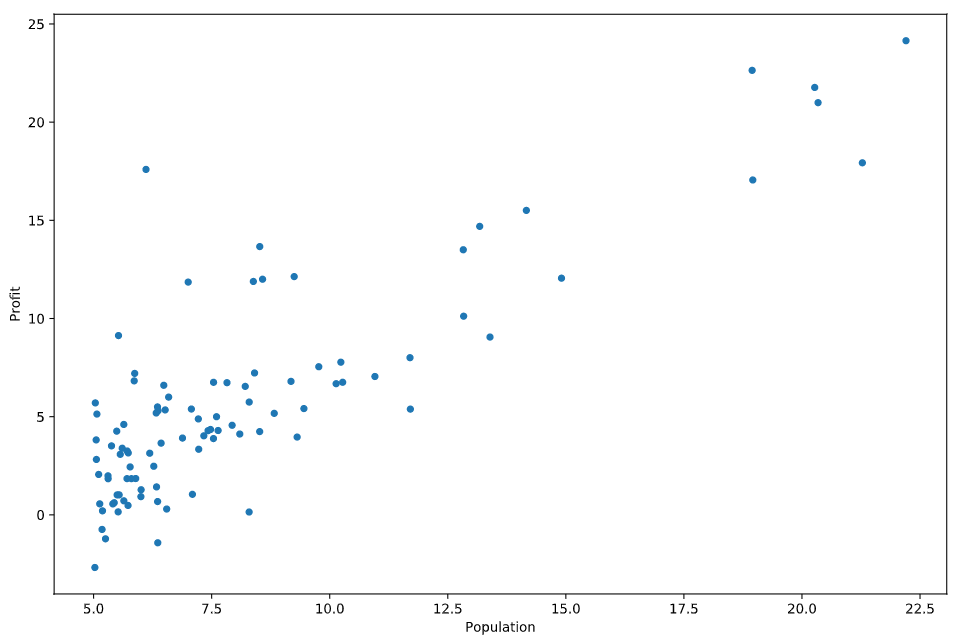

梯度下降知识点回顾

作业中把梯度下降方法分成了两个函数,一个是单变量的线性回归,一个是多变量的线性回归,这里是直接实现的是多变量的线性回归。

代价函数为:

  • 单变量
    $J\left( {\theta_{0}},{\theta_{1}}…{\theta_{n}} \right)=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}$
  • 多变量
    $J(\theta ) = \frac{1}{2m}(X\theta -y)^{T}(X\theta -y)$
    s.t. $h_{\theta}(x)=\theta^{T}X={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+…+{\theta_{n}}{x_{n}}$
    对$J$求导后,得到梯度下降更新算法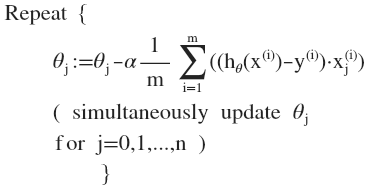

    注意这里的每个$\theta_{j}$都需要同时更新
    每次迭代计算后,每个$\theta_{j}$会趋于最优值,进而达到最低的cost,从而达到收敛

设置X,y,theta并转为numpy矩阵

实现过程中,我们设$X$为列向量,为了更方便的计算(向量化),考虑$\theta_{0}$,在$X$中插入每个元素为1的列向量,这样我们就可以轻易的使用代码来实现$h_{\theta}(x)=X \cdot\theta^{T}$来计算$h_{\theta}(x)$了

1
2
3
4
5
6
7
8
data.insert(0,'Ones',1)
cols = data.shape[1]
X = data.iloc[:,0:cols-1] # X是前cols-1列
y = data.iloc[:,cols-1:cols]#y是最后一列
#将X y theta转换为numpy矩阵
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0]))

def computeCost()

函数中前面注释的三行是计算单变量的,后面两行是计算多变量的

1
2
3
4
5
6
7
8
def computeCost(X, y, theta):
#
#    prediction = X * theta.T 
#    sqrErrors = np.power(prediction-y,2)
#    return np.sum(sqrErrors) / (2*len(X))
    prediction = X * theta.T 
    return (prediction-y).T * (prediction-y) / (2*len(X)) 
computeCost(X,y,theta)

执行函数后,结果是32.072733877455676

def gradientDescent

对于每个样本都需要计算,这里应该是batch gradient decent
$\theta _{j}:= \theta _{j} - \alpha \frac{\partial }{\partial \theta _{j}}J(\theta )$
注意每次更新都需要同时更新每个$\theta _{j}$
吴恩达老师的课特意强调了向量化,它可以让我们有更少的代码量(减少循环),同时也能利用高级语言的函数库更加快速的计算(如矩阵运算,可能可以实现并行计算等)
向量化的更新为
$\theta:=\theta-\alpha \cdot \delta$

1
2
3
4
5
6
7
8
9
10
11
12
def gradientDescent(X, y, theta, alpha, num_iters):

    J_history = np.zeros(num_iters)
    
    for i in range(num_iters):
        prediction = X * theta.T 
        delta = X.T * (prediction-y) / len(X)
        theta = theta - alpha * delta.T 
        # print(theta)
        J_history[i] = computeCost(X, y, theta)
        
    return theta, J_history

调用函数执行:
1
theta, J = gradientDescent(X, y, theta, alpha, num_iters)

theta = matrix([[-3.63029144, 1.16636235]])

画出拟合的回归方程以及代价函数的变化

前面我们虽然用来多变量的计算代价函数和梯度下降,但是当我们使用单变量时,我们还可以画出回归线性模型,看看他的拟合效果.

1
2
3
4
5
6
7
8
9
10
X = np.linspace(data.Population.min(), data.Population.max(), 100)
y = theta[0,0] + (theta[0,1] * X)
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(X, y, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

上述代码运行完,图像是这样的:

如何确定梯度下降已经正确的执行了?
**在每个迭代之后,$J(\theta)$应该在减小

  • 我们可以画出图像来看$J(\theta)$是否收敛
  • 我们还可以设置当$J(\theta)$在某个迭代计算中小于某个值来认为收敛,不过这个值难以确定,因为不同模型的$J$最小值可能是不一样的

下面我们画出代价函数的变化

1
2
3
4
5
6
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(num_iters), J, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

图像是这样的:

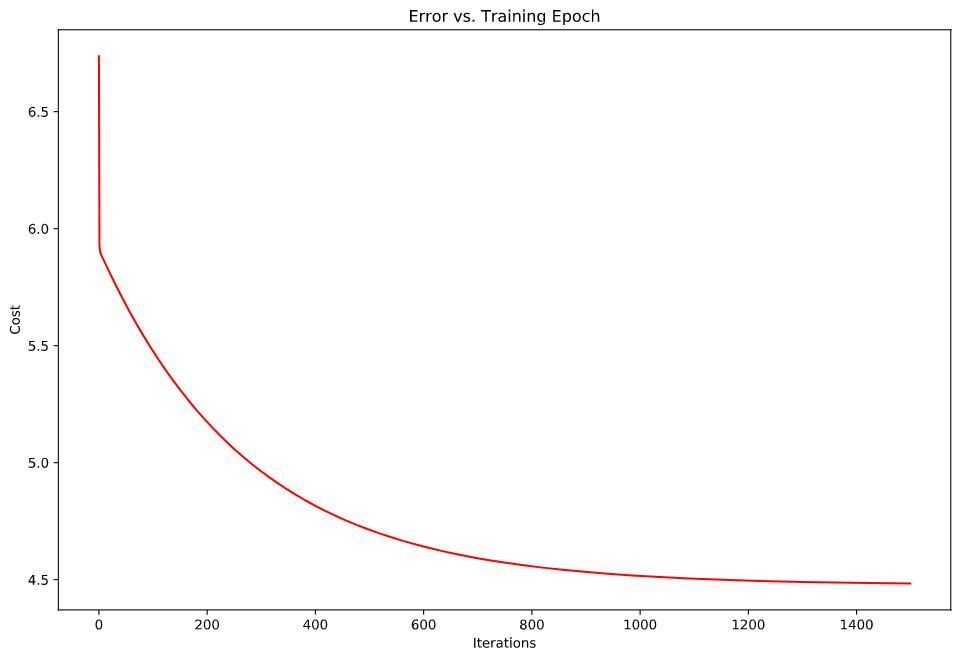
到这里,已经可以完成coursa上面的作业了
不过这里有个小细节需要注意:
$\alpha$(学习率)对梯度下降的收敛是有影响的,可以去不同的学习率来测试,我尝试过使用$\alpha=0.1$在单变量的环境下测试,是不会收敛的,一开始还以为是代码哪里写的有问题,后面想到学习率对于梯度下降的影响才恍然大悟。

关于$\alpha$(学习率)对梯度下降的影响:

  • $\alpha$太小: 慢收敛

  • $\alpha$太大:$J(\theta)$在每次迭代过程中可能不会减小,也可能不会收敛(当然也可能会慢收敛)
    如果我们的$J(\theta)$与iterations的图像是下面这样的,说明梯度下降没有很好的工作,需要使用更小的$\alpha$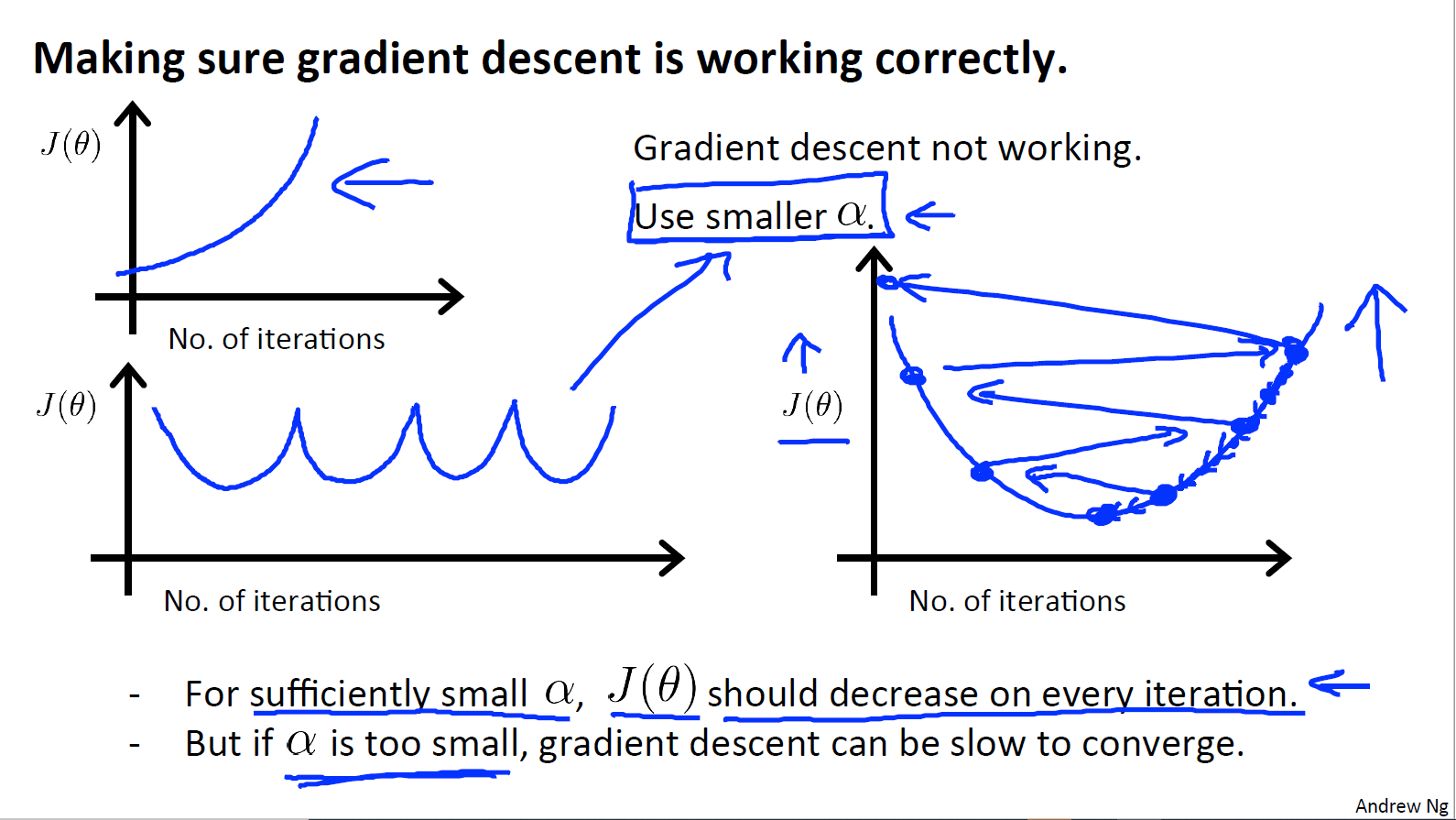

    实际计算过程中,我们可以尝试选择下面的$\alpha$来计算:

    …0.001,0.003,0.01,0.03,0.1,0.3,1…
    (每次$\times 3$)

下面是关于 特征缩放、正规方程的内容。

特征缩放(feature scaling)

前面的过程我们并没有将特征进行缩放,使用特征缩放在我们面对多维特征问题的时候,保证这些特征都具有相近的尺度,这将有助于梯度下降算法更快地收敛(如果特征差距过大,变量非常不均匀时,它会无效率地振荡到最优质,梯度下降算法需要非常多次的迭代才能收敛)

特征缩放一般是将数据减去均值再除以标准差,当然除以数据的最大与最小值之差也是可以的
一般来说特征缩放不需要太精确,只需要每个特征roughly the same,这样梯度下降可以运行的更快一些。
对于第二个实验数据的正则化,使用python可以这样完成

1
2
3
4
5
6
7
8
path = 'ex1data2.txt'
data2 = pd.read_csv(path,header=None,names=['Size','Bedrooms','Price'])
# data2.head()
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
X2 = (X2-X2.mean()) / X2.std()
X2.insert(0, 'Ones', 1)
y2 = data2.iloc[:,-1]

正规方程(Normal equation)

$\theta = (X^{T}X)^{-1}X^{T} \vec{y}$
直接使用这个公式就可以计算出让$J(\theta)$取值最小的$\theta$
注意使用正规方程计算不需要对X进行feature scaling
由上面的式子我们可以看出,正规方程主要工作量是在于计算:
$(X^{T}X)^{-1}$,计算机计算逆矩阵大约是$O(n^{3})$
一般情况下我们是不会出现$(X^{T}X)^{-1}$不存在(逆矩阵不存在)的情况
如果出现不可逆的情况,可以考虑:

  • Redundant features:有冗余特征,他们是线性相关的,这时候可以考虑去除冗余特征
  • too many features:假设我们有m个样本,n个特征。如果$m<n$,可能情况是m个样本不够来拟合n个特征的$\theta$,所以可以考虑减少特征数量,还有一种办法是regularization,它可以让我们在很少的样本时拟合很多的特征(这个方法吴恩达老师只是简单的介绍,具体应该会在后面的课程中讲述)
    第三周课程更新:
    (通过添加正则化项,我们还解决了存在不可逆矩阵的问题)

下面是具体的代码实现

1
2
3
def normalEqn(X, y):
    theta = np.linalg.inv(X.T@X)@X.T@y#X.T@X等价于X.T.dot(X)
    return theta

这里也需要注意一下,使用正规方程求出来的$\theta_{1}$和我们用梯度下降法求出来的$\theta_{2}$可能是不一样的
可以从等高线图来理解,或者老师课上的可视化代价函数,可能有多个$\theta$使得代价函数的最小的。
关于正规方程的推导过程我将会在另外的博客中进行说明,因为里面同样涉及到矩阵求导,还有PCA的优化求导,以及我的PR课上老师要求的一个求导小练习一起做个总结。
最后是梯度下降与正规方程的比较

梯度下降 VS 正规方程

Gradient Descent Normal equation
需要选择$\alpha$ 不需要选择$\alpha$
需要多次迭代计算 不需要迭代计算
当n(特征数量)很大时依旧工作的很好 需要计算$(X^{T}X)^{-1}$逆矩阵的计算需要$O(n^{3})$,通常来说当n小于10000 时还是可以接受的
适用于各种模型的优化求解 只适用于线性模型，不适合逻辑回归模型等其他更加复杂模型

bty,在batch gradient decent中复杂度是$O(m \times n) \approx O(n^{2})$