本篇博客的主要内容有:
- 反向传播算法(BackPropagation)
- python代码实现EX4的练习(使用BackPropagation来学习优化代价函数)
这篇博客的主要来源是吴恩达老师的机器学习第五周的学习课程,还有一些内容参考自黄海广博士的笔记GitHub,我先根据作业完成了matlab代码,并且学习将它用python来实现(博客中无matlab实现)。在学习的过程中我结合吴恩达老师的上课内容和matlab代码修改了一部分代码(个人认为可以优化的地方)。
这次的作业花了挺多的时间,首先是在于反向传播算法的学习(不是很好理解),接着实现matlab的代码花了一部分的时间,花较多的时间在python代码编写上(出现某个bug不能解决),好在最后还是顺利的完成了。
Neural Networks: Learning:反向传播算法(BackPropagation)
Cost Funciton
网络结构表示约定:
- L:网络的层数
- $s_{l}$: $l$层网络的单元数目(不包含添加的bias unit)
- $k$: 类别个数
对于二分类问题(binary classification):
有1个 outp unit
那么我们就有
- $s_{l}$ = 1
- $k$ = 1
对于多分类问题(Multi-class classific)(k classes)
有k output units
$y \epsilon R^{k}$
我们会将y写成例如下面的形式
$\begin{bmatrix}
1
\\
0
\\
0
\\
0
\end{bmatrix}$
表示为: 当样本有4个类别时,数字为1的索引表示该样本在第几类(具体的实现的话可以使用sklearn中的one-hot编码)
对于代价函数的定于,我们有:
$J(\theta) =
\frac{1}{m}\sum_{i=1}^m
\sum_{k=1}^K
\left[ -y^{(i)}_k \log((h_{\theta}(x^{(i)})_k)- (1 -y^{(i)}_k) \log(1-(h_{\theta}(x^{(i)}))_k) \right]
\\ \qquad
+\frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_{l}}\sum_{j=1}^{s_{l+1}}{\left( \Theta_{j,i}^{(l)}\right)^2} $
这个式子看起来很复杂,实际上它和我们之前讨论的逻辑回归是一样的,只是我们多了求和。
其中前面一项的求和可以这样理解:
假设我们只有一个样本,那么将样本输入,将会有k个output uint,实际上每个unit都是一个逻辑回归的$h_{\theta}(x)$,这样就有k个代价函数累加,m个样本的话就把每个样本的代价都求和即可后一项的求和实际上就是把网络中的$\theta$(除了bias之前)的每一项都平方求和,这是正则项,和逻辑回归的也是类似的
BackPropagation Algorithm
反向传播算法不容易理解,这里没有详细的介绍反向传播算法的思想,但是我会贴出一些图片或者链接(我推导的过程中参考的博客、视频等)
首先,我们的神经网络要学习,其优化目标就是:
$min_{\Theta}J(\Theta)$
那么我们就需要求得:
- $J(\Theta)$
- $\frac{\partial }{\partial \Theta_{j,i}^{(l)}}J(\Theta)$
求出梯度后,我们就可以使用梯度下降或者别的优化算法来学习
具体的推导过程可以参考这个视频:
斯坦福机器学习反向传播(Backpropagation)的数学推导
这位up貌似是中国人,但是录了英文视频,其中里面求出来的$\delta^{4}$up少了个负号,是因为他的代价函数那边少了一个负号
下面是couresa的社区提供的数学推导:
接下来你可以看看这个:
Back Propagation算法推导过程这个相对来说更加抽象化的推导
我还看了西瓜书的推导还有网上的一些博客,但是真正让我能够接受的就是前面这些了
想要体会为什么是反向传播,可以参考下面的知乎回答:
如何直观地解释 backpropagation 算法? - Anonymous的回答 - 知乎
反向传播算法的计算过程如下:
总结来说,使用bp学习的过程如下:
Gradient Checking(梯度校验,验证bp算法实现是否正确)
梯度校验实际上是使用数学上面偏导数的定义来求梯度,而反向传播实际上也是求梯度(偏导数),当我们的bp实现正确的时候,这两个梯度应该是相当接近的(误差<1e-9)
bp算法实现步骤较多,容易出错,使用梯度校验非常重要!
实现的是否,一般是先将每层的$\theta$合并成一个列向量,然后
求$\frac{\partial}{\partial\theta_i}J(\theta)$

$f_i(\theta) \approx \frac{J(\theta^{(i+)})-J(\theta^{(i-)})}{2\epsilon}$
从上面的公式来看,实际上即为用偏导数的定义来求梯度
具体实现的时候,计算每一个维度的$\theta$计算两次cost function(J),这使得计算量非常大,计算非常慢,这也是它不适合用来做为神经网络学习算法的原因之一,所以我们实现的时候,可以选择小型的网络来计算,当我们的bp算法正确实现的时候,就可以不再使用它了
Random Initialization
对于$\Theta$的初始化,我们不能简单的全都赋值为0,如下图所示:
如果我们令所有的$\theta$都为0(或者其他相同的值),那么我们的第二层所有激活单元都会有相同的值,最后bp中求得的$\delta$也都会是相同的值,那么我们的隐藏层可以认为是只有一个unit,这样网络结构就失去了意义,不同的unit学习不到不同的特征了,因此为了symmetry breaking,我们可以随机初始化每个参数在$[-\epsilon_{init},\epsilon_{init}]$范围之间,这个范围能够让每个参数值都较小并且能够让网络学习更加高效
$\epsilon_{init}$的值可以取为:
$\epsilon_{init} = \frac{\sqrt{6}}{\sqrt{L_{in}+L_{out}}}$
$L_{in} = s_l,L_{out} = s_{l+1}$
python代码实现
EX4中我们将再次处理手写数字数据集,我们将通过反向传播算法实现神经网络成本函数和梯度计算的非正则化和正则化版本,实现随机权重初始化和使用网络进行预测的方法。数据和EX3中是一样的
读入数据 定义sigmoid函数
1 | import numpy as np |
对y(labels)进行one-hot编码
1 | from sklearn.preprocessing import OneHotEncoder |
前面五条数据是这样的1
2
3
4
5[[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]]
也就是说,前面五个样本都是属于第10类
我们的网络架构是下图所示:
input是400(20*20) + 1(bias)
hidden是25 + 1(bias)
output是10(对应10个类别)
前馈神经网络
我们先定义forward_propagation函数,用来计算a1,z2,a2,z3,h
1 | def forward_propagation(X,Theta1,Theta2): |
Cost Function
下面求$J$
$J(\theta) =
\frac{1}{m}\sum_{i=1}^m
\sum_{k=1}^K
\left[ -y^{(i)}_k \log((h_{\theta}(x^{(i)})_k)- (1 -y^{(i)}_k) \log(1-(h_{\theta}(x^{(i)}))_k) \right]
\\ \qquad
+\frac{\lambda}{2m} \left[\sum_{j=1}^{25}
\sum_{k=1}^{400} {\left( \Theta_{j,k}^{(1)}\right)^2}+
\sum_{j=1}^{10}
\sum_{k=1}^{25} {\left( \Theta_{j,k}^{(2)}\right)^2}\right]$
循环里面的代码注释的是我自己写的,然后为注释的是参考黄博github的代码,有个问题就是我自己写的,在某些时候,会报log函数里面变成了0的情况(不懂是为啥)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def nn_cost_function(nn_params,input_size,hidden_size,num_labels,X,y,lambdaa):
m = X.shape[0]
X = np.array(X)
y = np.array(y)
Theta1 = np.array(np.reshape(nn_params[:hidden_size*(input_size+1)],(hidden_size,(input_size+1))))
Theta2 = np.array(np.reshape(nn_params[hidden_size*(input_size+1):],(num_labels,(hidden_size+1))))
a1,z2,a2,z3,h = forward_propagation(X,Theta1,Theta2)
J = 0
for i in range(m):
# cost = -y[i] @ np.log(h[i]) - (1-y[i]) @ np.log(1-h[i])
# J += cost
first_term = np.multiply(-y[i,:], np.log(h[i,:]))
second_term = np.multiply((1 - y[i,:]), np.log(1 - h[i,:]))
J += np.sum(first_term - second_term)
reg = np.sum(np.power(Theta1[:,1:],2)) + np.sum(np.power(Theta2[:,1:],2))
J = J / m + reg *lambdaa / (2 * m)
return J
下面我们载入EX3的weights数据,用来验证我们的J计算是否正确1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17data2 = loadmat('ex4weights.mat')
Theta1 = np.array(data2['Theta1'])
Theta2 = np.array(data2['Theta2'])
# forward_propagation(X,Theta1,Theta2)
input_size = 400
hidden_size = 25
num_labels = 10
lambdaa = 0.5
X = np.array(X)
y = np.array(y)
nn_params = np.concatenate([Theta1.flatten(),Theta2.flatten()])
# print(nn_params.shape) # 10285 *
print(nn_cost_function(nn_params,input_size,hidden_size,num_labels,X,y_onehot,lambdaa))
实现的时候注意先实现未添加正则项的,再实现添加正则项的
使用练习中给出的Theta1,Theta2,算出来的J=0.28762916516131876(lambdaa=0)
使用练习中给出的Theta1,Theta2,算出来的J=0.3837698590909235(lambdaa=1) 添加了正则项
定义sigmoid_gradient,rand_initialize_weights函数
$g’(z)=\frac{d}{dz}g(z) = g(z)(1-g(z))$
$\mathrm{sigmoid}(z)=g(z)=\frac{1}{1+e^{-z}}$
1 | def sigmoid_gradient(z): |
bp算法
bp算法的实现可以参考这张图:
使用np.matrix好像可以用更短的代码实现,不过我使用了np.array,所以有些需要reshape,导致代码有点复杂
这里面我debug了好久的问题有两个:
- 我将计算$\delta^{(2)}$ 的代码中sigmoid_gradient函数写成了simgoid
1
delta2 = np.multiply((Theta2.T @ delta3.T).T ,sigmoid_gradient(z2t))
在bp对每个样本循环的时候,为了调试,我只先求了第一个样本的,导致最后的梯度计算不对
正则化项注意验证
1 | def back_propagation(nn_params,input_size,hidden_size,num_labels,X,y,lambdaa): |
写好bp函数后,我们就应该使用gradient checking了
gradient checking
1 | def check_nn_gradient(lambdaa = 0): |
写代码的时候,需要注意的有,传入的X是已经插入了一列为1的,还是没有插入,我一般情况下使用在函数里面insert
下图可以看到,我们的梯度和bp的梯度基本上是接近的,说明我们的bp实现是正确的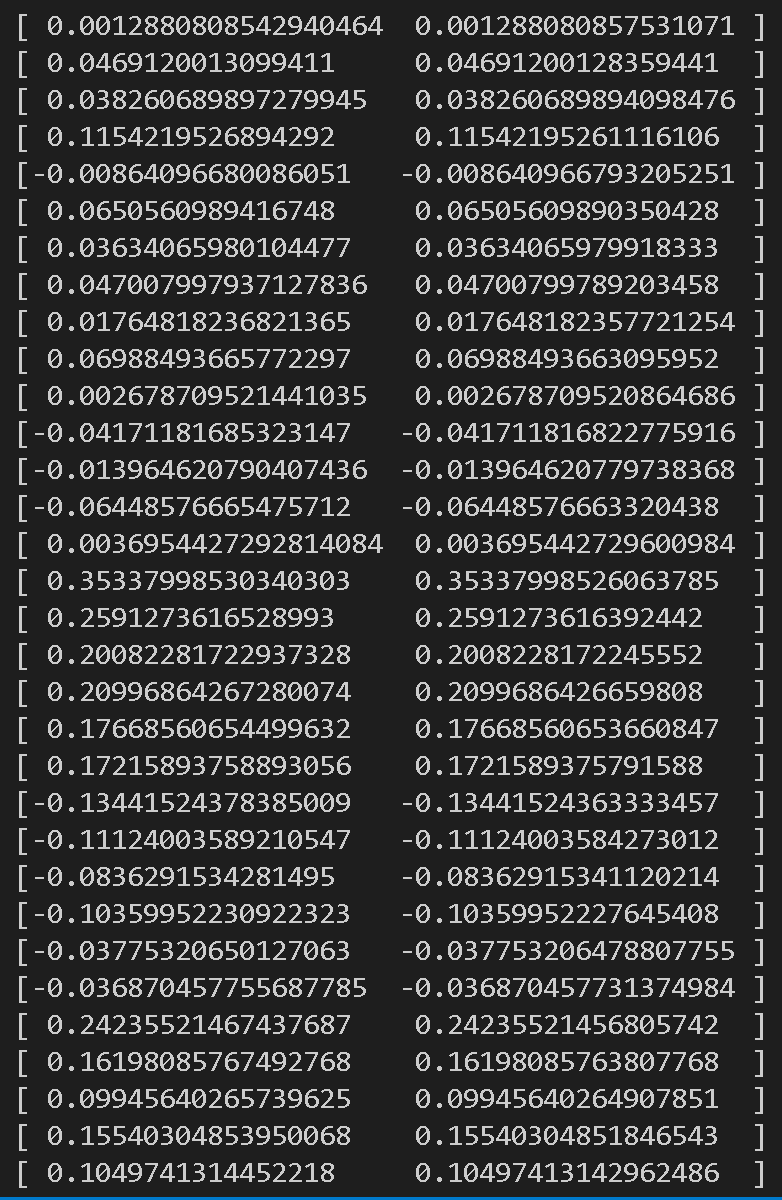
注意$\lambda=0$是无正则项的验证,我们还需要验证$\lambda=1$情况,只有通过了梯度验证,我们才能继续
接下来就使用优化函数求最优$\Theta$,并且求准确率了
优化目标函数求准确率
1 | from scipy.optimize import minimize |
总结
关于numpy中的乘法
元素乘法:np.multiply(a,b)
矩阵乘法:np.dot(a,b) 或 np.matmul(a,b) 或 a.dot(b) 或直接用 a @ b !
唯独注意:*,在 np.array 中重载为元素乘法,在 np.matrix 中重载为矩阵乘法!梯度验证和one-hot表示值得记录学习
References
完整代码
1 | import numpy as np |