本篇博客的主要内容有:
- 前馈神经网络理论知识
- python代码实现EX3的练习(逻辑回归多分类器构建,前馈神经网络的实现)
这篇博客的主要来源是吴恩达老师的机器学习第四周的学习课程,还有一些内容参考自黄海广博士的笔记GitHub,先根据作业完成了matlab代码,并且学习将它用python来实现(博客中无matlab实现)。在学习的过程中我结合吴恩达老师的上课内容和matlab代码修改了一部分代码(个人认为可以优化的地方)。
Neural Networks: Representation
Non-linear Hypotheses
线性回归和逻辑回归都有这样一个缺点:当特征太多时,计算的负荷会非常大。
如果对逻辑回归印象模糊的话,需要去看看吴恩达老师前面的课程,因为它是神经网络的基础。
在前面的练习过程(EX3)中,我们通过添加多项式项来作为特征来训练,构造非线性分类器来预测。
但是,如果我们有非常多的特征,那么构造非线性多项式的分类器会产生非常多的特征组合。
例如: 我们有$n$个特征,即使我们使用两两相乘作为特征组合($x_{1}x_{2},x_{1}x_{3},…x_{99}x_{100}$),那么我们会组成$C_{n}^{2}\approx 5000$个特征,数量过多的特征不仅可能导致过拟合,并且计算代价也是相当大的
因此,用Quadratic features来找Non-linear boundary不是一个好办法
也就是说,普通的逻辑回归模型,不能有效地处理这么多的特征,这时候我们就可以考虑使用神经网络了。
Model Representation
我们大脑的神经网络一般是这样的:
神经元含有许多的树突(输入),神经元处理计算后,通过轴突(输出)传给其他的神经元,这些神经元共同组成了大脑的神经网络。
在机器学习中,我们将使用逻辑回归模型作为我们的神经元模型:(Logistic Unit) (activation unit or 激活单元)来构建神经网络,如下图所示: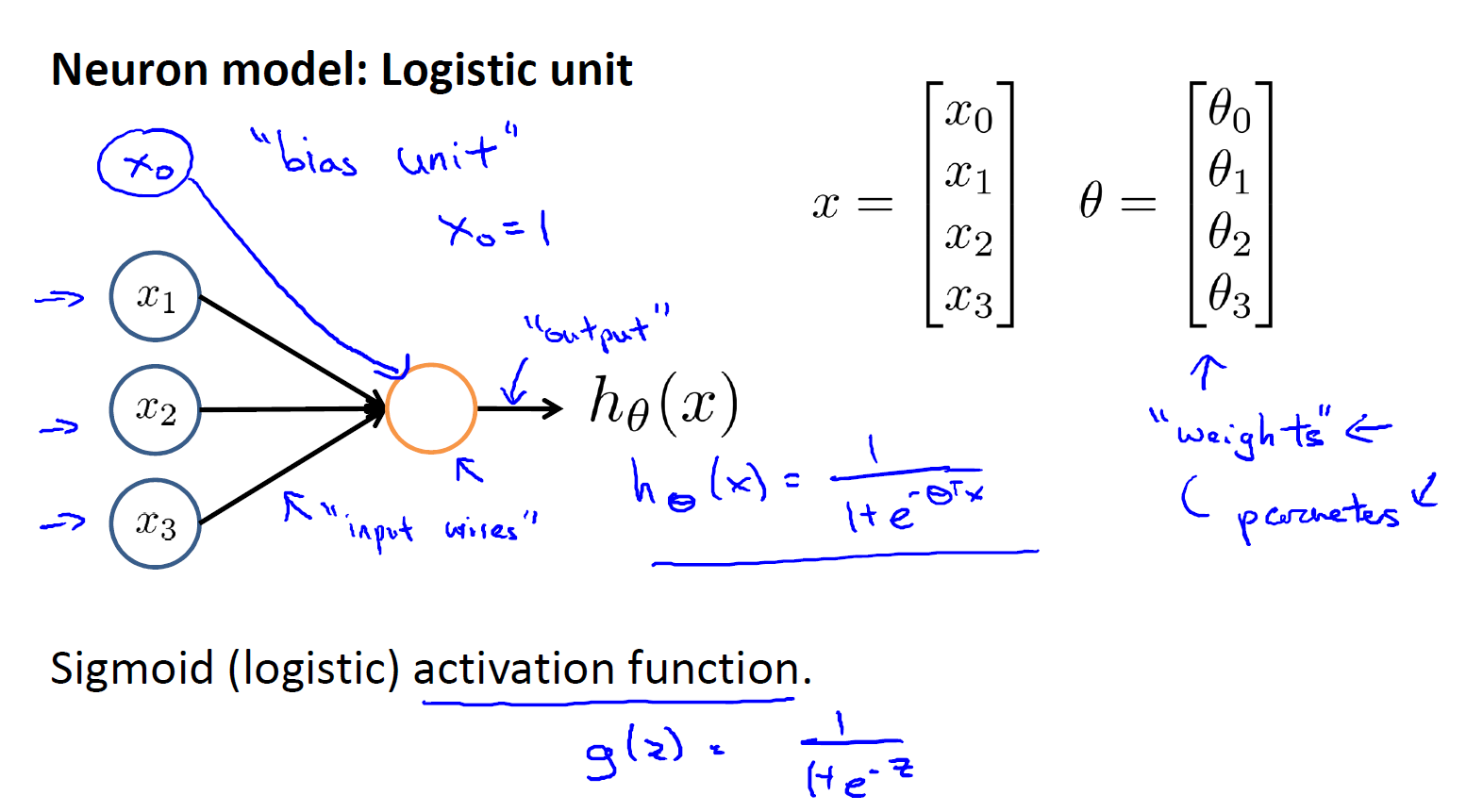
这与我们之前学过的逻辑回归模型是一样的,用它构建的神经网络可以是下面这样的:
用逻辑单元构建的神经网络,每一层的输出作为下一层的输入。上图为是一个3层的神经网络,
第一层是输入层 (Input Layer) ,
最后一层是输出层(Output Layer) ,
除了输入输出层之外,我们统称为隐藏层(Hidden Layers)。
注意,这里我们我们为每一层都增加一个bias unit,就好像是在线性回顾和逻辑回归中的$\theta_{0}$一样
为了更好的表示神经网络模型和向量化,我们使用下面的表示:
$a_{i}^{(j)}$ = “activation” of unit i in layer j
即: 第j层的第i个激活单元
$\Theta ^{(j)}$ = matrix of weights controling function mapping from layer j to layer j+1
即 用一个$\Theta$矩阵来表示:控制从第j层到底j+1层映射的权重矩阵
即 $\Theta^{(1)}$表示从第1层映射到第二层的权重矩阵
$\Theta_{1i}^{(1)} (i从0到n)$表示从第1层映射到第2层的$a_{1}^{(2)}$的权重,也就是单个逻辑回归单元的$\theta_{0}\sim \theta_{3}$
因此,如果网络的第$j$层有$s_{j}$个单元,在第$j+1$层有$s_{j+1}$个单元,那么$\Theta$的维度是$s_{j+1} \times (s_{j} + 1)$
之所以要$+1$是对每个$a_{1}^{(2)},a_{2}^{(2)},a_{3}^{(2)}$ 添加一个bias unit(可以认为是$\theta_{0}$)
foward propagation
下面我们就进行神经网络的一层一层(从输入到输出)传播的计算(也就是前馈神经网络),为了更好的进行代码实现,我们需要进行向量化表示,它不仅能够大量减少我们的代码量,还可以让我们的程序使用计算库来计算(这些计算库可能会有做矩阵运算的优化,进行并行计算等等)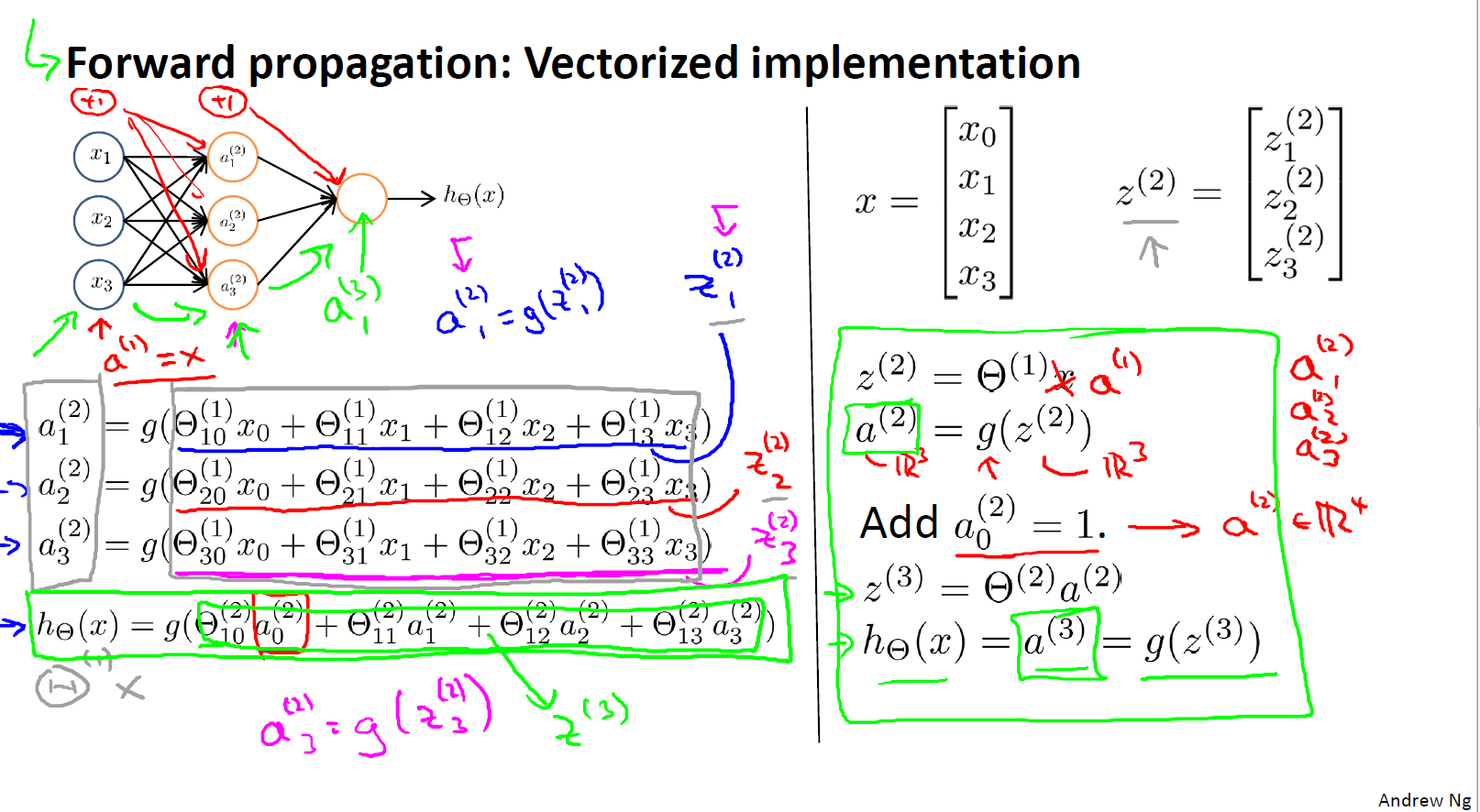
上图为前馈神经网络的计算过程,我们设数据为
$x = \begin{bmatrix}
x_{0}
\\
x_{1}
\\
x_{2}
\\
x_{3}
\end{bmatrix}$
$z^{(2)} = \begin{bmatrix}
z_{1}^{(2)}
\\
z_{2}^{(2)}
\\
z_{3}^{(2)}
\end{bmatrix}$
$z^{(2)} = \Theta^{(1)} x = \Theta^{(1)} x a^{(1)}$
经过sigmoid函数计算后:
$a^{(2)} = g(z^{(2)})$
这里都是使用矩阵统一向量化计算的,不需要单独求$a_{1}^{(2)},a_{2}^{(2)},a_{3}^{(2)}$
得到$a^{(2)}$之后,我们还需要添加 $a_{0}^{(2)} = 1$
所以 神经网络就像是逻辑回归,只是我们把逻辑回归中的输入向量$[x_{1},x_{2},x_{3}]$ 变成了中间层的$[a_{1}^{(2)},a_{2}^{(2)},a_{3}^{(2)}]$,然后我们需要添加逻辑回归中的$\theta_{0}$
但是和逻辑回归不同的是,逻辑回归受输入的原始特征$[x_{1},x_{2},x_{3}]$的限制,即使我们用多项式来组合这些特征,我们依旧受原始特征的限制,当神经网络不同,神经网络能从输入中学习自己的特征$[a_{1}^{(2)},a_{2}^{(2)},a_{3}^{(2)}]$,再将它输入逻辑回归单元中,神经网络具有更强的灵活性
下面是前馈神经网络的计算总结:
$z^{(j)} = \Theta^{(j-1)} a^{(j-1)}$
$a^{(j)} = g(z^{(j)})$
$z^{(j+1)} = \Theta^{(j)} a^{(j)}$
$h_{\theta}(x) = a^{(j+1)} = g(z^{(j+1)})$
神经网络能够构造更加复杂的函数,不断学习新的特征,新的更复杂的特征,进而不断层次深入,让我们的逻辑回归分类器能够做出更准确的预测,下面是两个例子对这句话的直观理解
Eaxmples
线性可分 实现AND逻辑运算
and运算是线性可分的,可以从下图来看: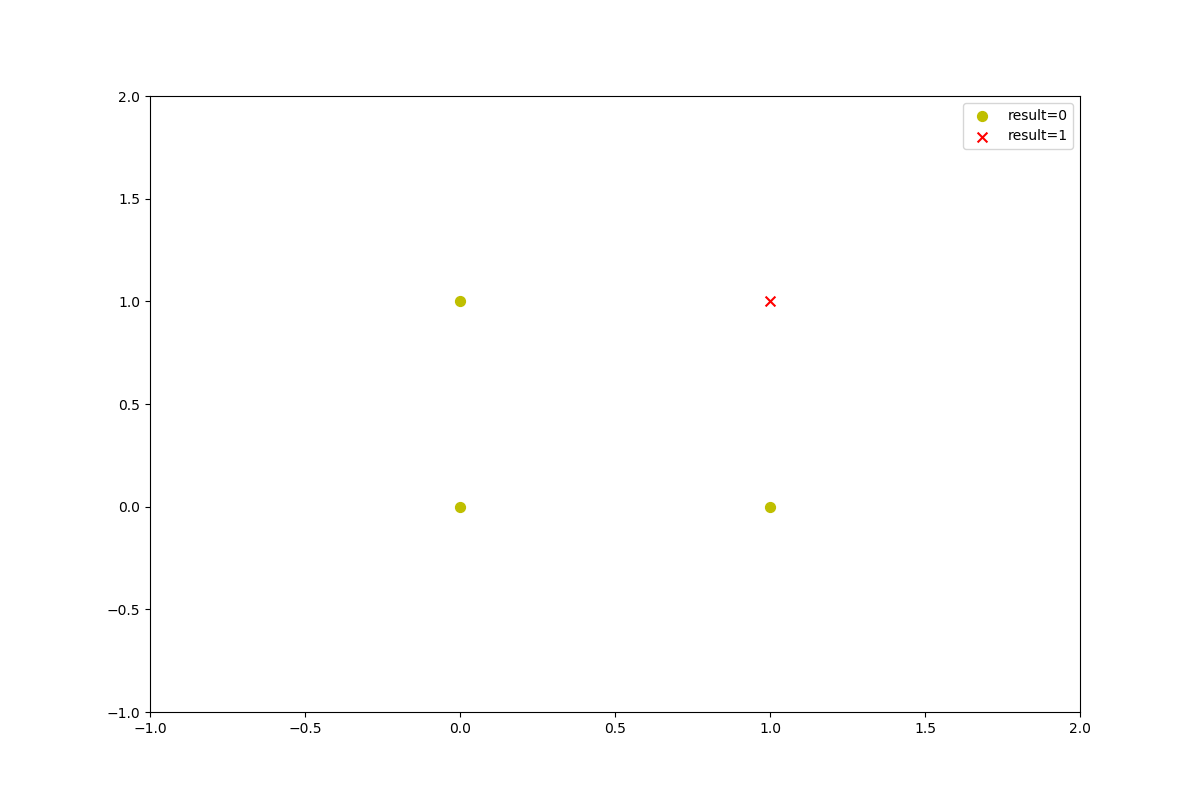
通过构造下面的神经网络模型,我们就可以让$h_{\theta}(x) \approx x_{1} and x_{2}$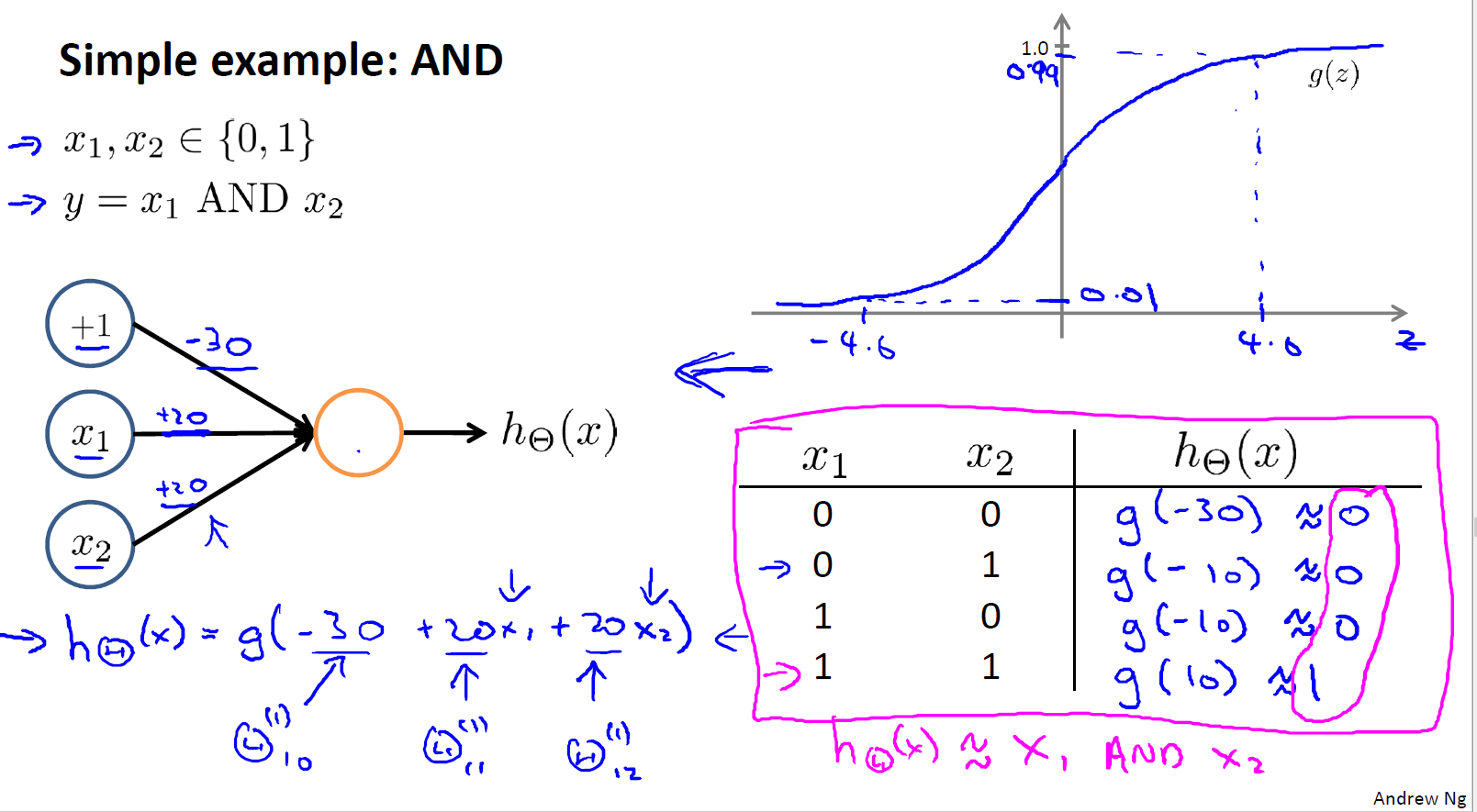
非线性可分 实现异或非(XNOR)
异或非的数据是这样子的(非线性可分):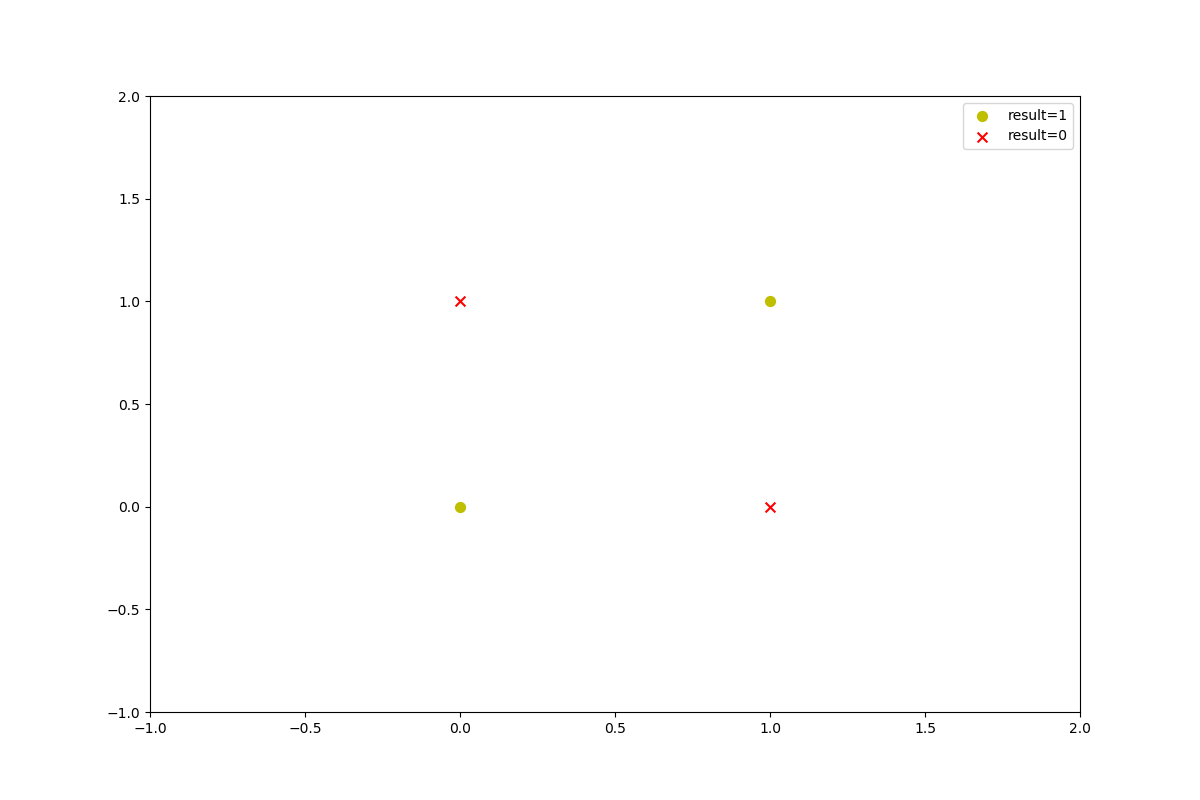
吴恩达老师通过联合多个逻辑单元,使得网络可以让$h_{\theta}(x) \approx x_{1} xnor x_{2}$
至于如何训练这些..后面的课程应该会说明
python代码实现
使用逻辑回归实现多分类
读入数据并可视化
由于作业中的数据集是.mat格式的,我们需要使用使用一个SciPy中的loadmat来加载它
数据是手写数字的图片,是5000400的,表示有5000张图片,然后400表示的是2020的图片,将灰度图像转为一个行向量就变成了400
1 | import numpy as np |
下面是可视化数据,参考了这篇博客
1 | def displayData(X): |
可视化结果如下图:
sigmoid cost grad函数
这三个函数和上次逻辑回归的作业添加正则项的没有差别,因此这里不再多说明了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19def sigmoid(z):
return 1 / (1 + np.exp(-z))
def lrCostFunction(theta,X,y,lambdaa):
h = sigmoid(X.dot(theta.T))
J =(- y.T .dot(np.log(h))-(1-y).T.dot(np.log(1-h) ))/len(X)
reg = theta[2:].T .dot(theta[2:] )* lambdaa / (2*len(X))
J = J + reg
return J
def lrGradFunction(theta,X,y,lambdaa):
grad = np.zeros(len(theta))
theta = theta.reshape(1,len(theta))
h = sigmoid(X.dot(theta.T))
reg = lambdaa * theta / len(X)
reg[0][0] = 0
grad = X.T.dot ((h-y)) / len(X) + reg.T
return grad
one_vs_all函数
下面我们定义一对多函数来实现多分类
实现多分类的思想是:
对于多分类问题,我们可以每次将一类样本当作一类,其他所有样本当作另外一类,c类样本的话总共需要c个分类器,当我们用来预测时,只需要将新的样本输入,然后选择c个分类器中概率最大的那个
下面是具体的代码实现:
这里面有几个地方需要注意下:
- 我们将X数据插入1矩阵,从5000400变为5000501
- 对于c个分类器,我们训练的时候,如果样本是属于第$w$类,那么我们就属于$w$类的y标记为1,其他所有的样本标记为0
- 使用SciPy的fmin函数来优化cost
- 计算过程中注意维度的不同,程序报错一般情况下是数据维度不一致导致不能相乘接下来我们定义预测函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14def one_vs_all(X,y,num_labels,lambdaa):
m = X.shape[0]
n = X.shape[1]
X = np.insert(X, 0, values=np.ones(m), axis=1) # X:5000 * 401
all_theta = np.zeros((num_labels,n+1))
for c in range(1,num_labels+1):
initial_theta = np.zeros((n + 1, 1))
binary_y = np.array([1 if label == c else 0 for label in y])
binary_y = np.reshape(binary_y, (m, 1))
fmin = minimize(fun=lrCostFunction, x0=initial_theta, args=(X, binary_y, lambdaa), method='TNC', jac=lrGradFunction)
all_theta[c-1,:] = fmin.x
return all_theta # 10 * 401
predictOneVsAll
1 | def predictOneVsAll(X, all_theta): |
这里函数返回的是h_argmax + 1,是因为,我们的类别预测返回的索引是从0开始的,但是我们的y是从1-10,并且0类对应的是第10类
接下里就可以计算模型的准确率了,构建数据调用函数
1 | num_labels = len(np.unique(y)) |
可以得到:
$\lambda = 0.1:$1
accuracy = 96.46%
接下来是前馈神经网络的实现
foward propagation
实现的时候注意矩阵维度,其他就是更加前面的传播总结写的代码
注意这里的数据$\Theta^{(1)},\Theta^{(2)}$都是作业给出的已经计算好的权重矩阵,这里的话直接使用即可1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17# Theta1 has size 25 x 401
# Theta2 has size 10 x 26
def predictFeedforwardPropagation(X,Theta1,Theta2):
m = X.shape[0]
num_labels = Theta2.shape[0]
X = np.insert(X, 0, values=np.ones(m), axis=1)
z2 = Theta1 @ X.T
a2 = sigmoid(z2) # 25 * 5000
print(a2.shape)
a2 = np.insert(a2, 0, values=np.ones((1,X.shape[0])), axis=0)
print(a2.shape) # 26 * 5000
z3 = Theta2 @ a2
h = sigmoid(z3) # 10 * 5000
# print(h.shape)
h_argmax = np.argmax(h,axis=0)
# print(h_argmax.shape) # 5000,
return h_argmax + 1
接下来使用神经网络分类:1
2
3
4
5
6
7
8data2 = loadmat('ex3weights.mat')
Theta1 = np.array(data2['Theta1'])
Theta2 = np.array(data2['Theta2'])
y_feed_pred = predictFeedforwardPropagation(X,Theta1,Theta2)
feed_correct = [1 if a == b else 0 for (a, b) in zip(y_feed_pred, y)]
feed_accuracy = (sum(map(int, feed_correct)) / len(feed_correct))
print ('accuracy = {:.2f}%'.format(feed_accuracy * 100)) # 97.52%
最后的准确率可以达到:1
accuracy = 97.52%
完整代码
1 | import numpy as np |