NG机器学习EX5(Evaluating a Learning Algorithm)

发表于 | 分类于 | | 热度: ℃
字数统计: 3.8k字 | 阅读时长 ≈ 19分钟

主要内容有：

  1. 模型选择、评价指标
  2. 绘制数据,欠拟合、过拟合曲线及学习曲线

这篇博客的主要来源是吴恩达老师的机器学习第六周的学习课程,还有一些内容参考自黄海广博士的笔记GitHub
我先根据作业完成了matlab代码,并将它用python来实现(博客中无matlab实现)
实现过程中我结合吴恩达老师的上课内容和matlab代码修改了一部分代码(个人认为可以优化的地方)

advice for applying machine learning

deciding what to try next

当我们使用一些新的测试集来测试我们已经训练好的模型时,如果出现较多的误差(分类错误或者 回归问题与正确预计值相去甚远),我们可以尝试:

  1. 获得更多的训练样本
  2. 减少/增加特征数量
  3. 减小/增大$\lambda$ 用来减少/增加正则化程度
  4. 添加多项式特征
    为了让我们知道应该尝试哪一种,我们需要评估机器学习算法性能,进行机器学习诊断(Diagnostic),来提高我们的算法性能
    Diagnostic可能需要花费一定的时间,但是这些时间是值得的,可能会起到事半功倍的效果

Evaluating a Hypothesis

如何判断模型是欠拟合还是过拟合呢
在2D的时候 我们可以通过画图来发现我们的hypothesis是否过拟合了,但是在高维数据下,想要通过画出hypothesis来进行观察，就会变得很难甚至是不可能实现。,因此我们需要另一种方法来评估
一般情况下,我们会将数据随机的划分为训练集和测试集,比如70%的数据用来训练,而30%的数据用来测试(来评价我们的模型的generalization ability)
具体地:
我们使用训练集来获得我们的parameters($\theta$),使用测试集来计算test set error
test set error一般是计算代价函数(J),对于逻辑回归(分类)的话,我们可以这样计算:
$J_{test}(\theta) = \frac{1}{m_{test}}\sum_{i=1}^{m_{test}}[-y_{test}^{(i)}log(h_{\theta}(x_{test}^{(i)}))-(1-y_{test}^{(i)})log(1-h_{\theta}(x_{test}^{(i)}))]$
我们还可以这样计算:
$J_{test}(\theta) = \frac{1}{m_{test}}\sum_{i=1}^{m_{test}}err(h_{\theta}(x)^{i},y^{(i)})$
其中$err(h_{\theta}(x),y) = \left\{\begin{matrix}
1 (if… h_{\theta}(x) \geq 0.5, y = 0).. or… (if…h_{\theta}(x) \leq 0.5,y=1)
\\
0 (othersize)
\end{matrix}\right.$

Model Selection and training/validation/test Sets

一般来说,当我们的模型发生过拟合时,我们的training error$J(\theta)$ 通常会比实际的generalization error低很多,因为我们训练的时候,我们的参数(parameters)总是在fit training set
我们应该如何选择我们的模型呢?
如果我们如上文一样,仅仅将数据分为training set和test set
假设我们有多组不同的参数,我们想要从中选出最优的,我们会怎么选择呢?
我们通常会选择test error最小的,作为我们模型的最优parametes
但是,如果我们使用的是test error最小的,那我们如何才能评估我们模型的泛化能力呢?(也就是获得定量的generalization error)

如果我们使用test error作为我们的generalization error会出现这样的问题:
吴恩达老师说:

$min J_{test}(\theta)$ is likely to be an optimistic estimate of generalization error i.e. our extra paramter(d = degree of ploynomial) is fit to the test set

这里d是多项式的次数,比如下面的

  1. $h_{\theta}(x) = \theta_{0} + \theta_{1}x$
  2. $h_{\theta}(x) = \theta_{0} + \theta_{1}x + \theta_{2}x^2$
  3. $h_{\theta}(x) = \theta_{0} + \theta_{1}x + \theta_{2}x^2 + \theta_{3}x^3$
    …
  4. $h_{\theta}(x) = \theta_{0} + \theta_{1}x + \theta_{2}x^2 +… \theta_{10}x^{10}$

也就是说 我们的模型实际上也从test set中学习了最优的参数,因此使用test error不能很好的衡量我们的generalization error

所以:
我们会将数据划分为三部分

  1. training set 如60%
  2. cross validation set 如20%
  3. test set 如20%
    接下来我们使用training set $J_{train}(\theta)$训练,找出最小的cross validation error $J_{cv}(\theta)$所使用的parameters,然后再用我们的模型来计算test error$J_{test}(\theta)$,用test error来作为评估我们的模型泛化能力的指标
    $J_{cv}(\theta)$一般会比$J_{test}(\theta)$小,因为an extra parameter(d) has been fit to the class validation set
    而 $J_{test}(\theta)$ 可以用来衡量泛化能力是因为:
    the degree of the ploynomial d has not been trained using the test set
    感觉翻译起来怪怪的,干脆直接贴英文吧

Diagnosing Bias vs. Variance

下面是High bias和High variance的示例图片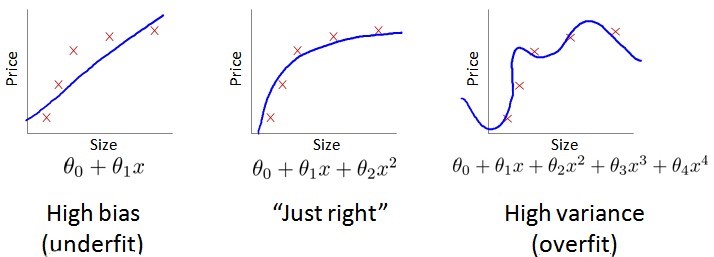

要判断是否发生了过拟合还是欠拟合,更一遍的情况下,我们会使用参数做横坐标,画出误差曲线,比如这里使用d,而下面的练习中会使用$\lambda$来绘制,如下图:

这里面比较重要的是:

  • High bias(underfiting): $J_{cv} \approx J_{train} $ ,并且这两个值都较高
  • High variance(overfitting): $J_{train}$低 并且 $J_{cv} \gg J_{train}$(两个值相差较大)

Regularization and Bias_Variance

在我们在训练模型的过程中，我们会添加正则化项来防止过拟合。但是$\lambda$的取值也是我们需要考虑的事情(和上面的d一样)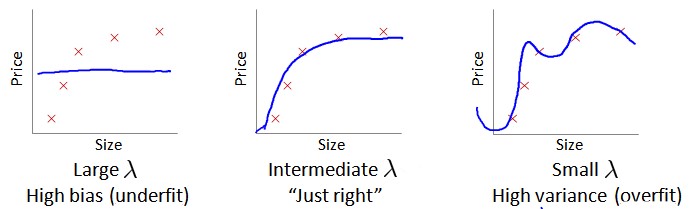

那么我们选择$\lambda$ 的方法如下:

  1. 创造一个list,里面是$\lambda$的各种取值:如:[0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24]
  2. 使用不同的$\lambda$来学习$\theta$(还可以选择不同的d来用不同的$\lambda$学习)
  3. 计算$J_{cv}$,这里的$J_{cv}$是不带正则化项的(或者说$\lambda=0$)
  4. 找出最小的$J_{cv}$模型M
  5. 使用M中的params,计算$J_{test}$来评估我们的模型是否具有泛化问题

需要注意的是,我们在计算$J_{cv},J_{train},J_{test}$中都不需要加入正则项,而在我们训练模型时的$J$需要加入正则化项,这样做的原因是为了减少过拟合

下图中: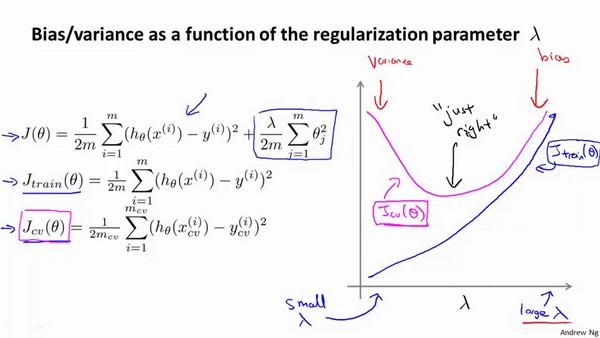

$\lambda$较小时,$J_{train}$较小(overfitting),$J_{cv}$较大
随着$\lambda$增大,$J_{train}$不断增加(under fitting),而$J_{cv}$是先减小后增大

Learning Curves

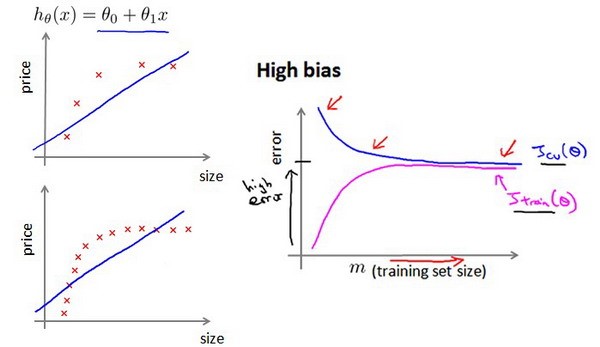
在high bias(underfit)下,添加更多的训练集不一定会起作用

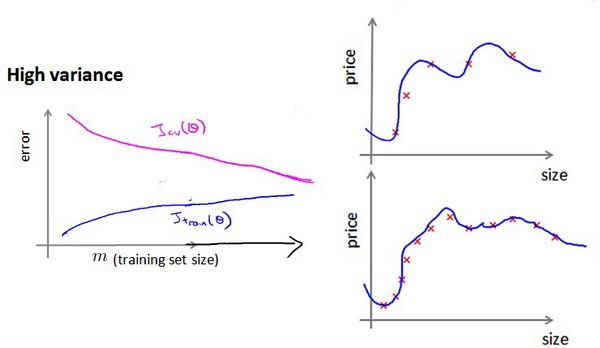
在high variance(overfitting)下,添加更多的训练集可能会是我们的模型表现的更好

Deciding What to Do Next Revisited

  • 获得更多的训练样本 — 解决high bias
  • 减少/增加特征数量 — 解决high variance/high bias
  • 减小/增大$\lambda$ — 解决high bias/high variance
  • 添加多项式特征 — 解决high bias

而对于神经网络而言:

  • parameters越少(小型网络),越容易欠拟合,但是计算代价小
  • parameters越少(大型网络),越容易过拟合,但是计算代价大

代码实现

代码中 导入数据集 计算线性回归的代价函数、梯度 训练线性回归模型在之前的练习中都有写过
下面是完成练习中主要实现的代码:

计算$J_{train},J_{cv}$

1
2
3
4
5
6
7
8
9
10
def learningCurves(Xtrain,ytrain,Xval,yval,lambdaa):
    m = Xtrain.shape[0]
    errorTrain = np.zeros((m,1))
    errorCv = np.zeros((m,1))
    for i in range(1,m+1):
        optTheta = trainLinearReg(Xtrain[:i,],y[:i],lambdaa)['x']
        errorTrain[i-1] = linearRegCostFunction(optTheta,Xtrain[:i,],ytrain[:i],0)
        errorCv[i-1] = linearRegCostFunction(optTheta,Xval,yval,0)

    return errorTrain,errorCv

还有一个代码是选做的,随机选择样本来绘制学习曲线

计算$J_{randomTrain},J_{randomCv}$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def randomLearningCurves(Xtrain,ytrain,Xval,yval,lambdaa):
    m = Xtrain.shape[0]
    randomErrorTrain = np.zeros((m,1))
    randomErrorCv = np.zeros((m,1))
    repeat = 50
    for r in range(repeat):
        for i in range(1,m+1):
            trainNum = i
            trainIndex = random.sample(range(0,m),trainNum)
            randomXtrain = Xtrain[trainIndex]
            randomYtrain = y[trainIndex]
            cvNum = i
            cvIndex = random.sample(range(0,m),cvNum)
            randomXcv = Xval[cvIndex]
            randomYcv = yval[cvIndex]
            # print(randomXtrain,randomYtrain)
            optTheta = trainLinearReg(randomXtrain,randomYtrain,lambdaa)['x']
            randomErrorTrain[i-1] = linearRegCostFunction(optTheta,randomXtrain,randomYtrain,0)
            randomErrorCv[i-1] = linearRegCostFunction(optTheta,randomXcv,randomYcv,0)
    randomErrorTrain = randomErrorTrain / repeat
    randomErrorCv = randomErrorCv/ repeat
    return randomErrorTrain,randomErrorCv

添加多项式特征

这个代码的写法具有学习意义,所以单独摘出来:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def normalizeFeature(df):
    return df.apply(lambda column: (column-column.mean())/column.std())


def  polyFeatures(x, power,as_ndarray=False):

    # construct dictionary and change it to dataFrame
    data = {'f{}'.format(i):np.power(x,i) for i in range(1,power+1)}
    df = pd.DataFrame(data)
    return df.to_numpy() if as_ndarray else df

def preparePloyData(*args,power):
    '''
    args: keep feeding in Xtrain, Xval, or Xtest will return in the same order
    '''
    def prepare(x):
        df = polyFeatures(x,power)
        ndarr = normalizeFeature(df).to_numpy()
        return np.insert(ndarr,0,np.ones(ndarr.shape[0]),axis=1)     
    
    return [prepare(x) for x in args]

接下来还需要注意的代码,就是画图了

我画出来的图像如下: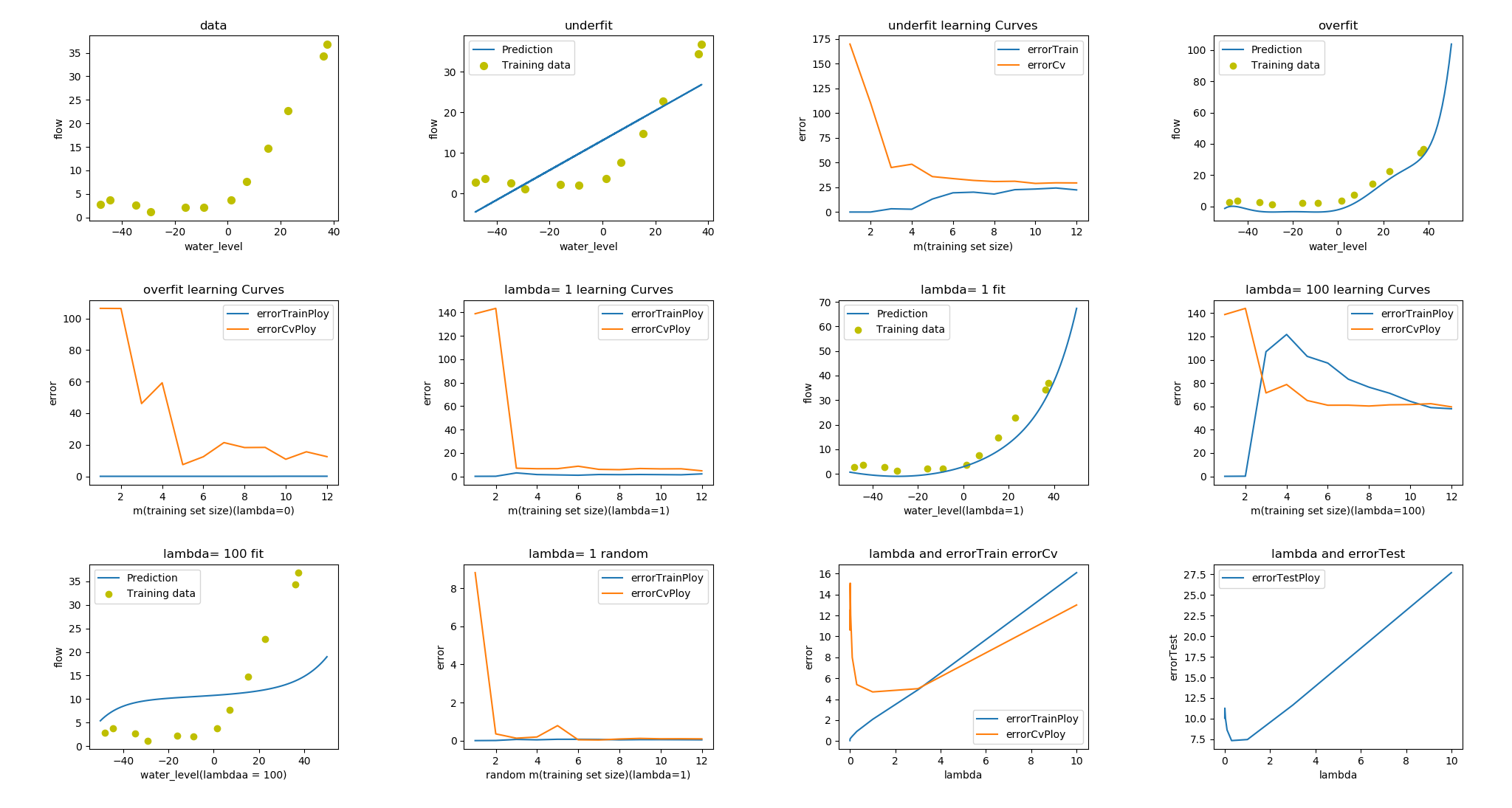

完整代码比较长,我将贴在本文的最后

References

  1. 黄海广博士的笔记GitHub

  2. 谷歌开发者:分类 (Classification)：精确率和召回率

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt 
from scipy.io import loadmat
import scipy.optimize as opt 
import random 


def loatData():
    data = loadmat('ex5data1.mat')
    X = data['X']
    y = data['y']
    Xval = data['Xval']
    yval = data['yval']
    Xtest = data['Xtest']
    ytest = data['ytest']
    return map(np.ravel,[X,y,Xval,yval,Xtest,ytest])
    # return X, y, Xval, yval, Xtest, ytest

# def plotDdata(X,y):
#     fg,ax = plt.subplots(figsize = (12,8))
#     ax.scatter(X,y,s=50,c='y',marker='x')
#     ax.set_xlabel('water_level')
#     ax.set_ylabel('flow')
#     plt.show()

def linearRegCostFunction(theta,X,y,lambdaa):
    m = X.shape[0]
    h = X  @ theta
    J = (h-y).T @ (h-y) / (2*m)
    reg = theta[1:].T @ theta[1:]
    J = J + reg * lambdaa / (2*m)
    return J 

def linearRegGrad(theta,X,y,lambdaa):
    m = X.shape[0]
    h = X  @ theta
    grad = X.T @ (h-y) / m
    gradReg = theta *lambdaa / m
    gradReg[0] = 0
    grad = grad + gradReg
    return grad

def trainLinearReg(X,y,lambdaa):
    theta = np.ones(X.shape[1])
    res = opt.minimize(fun=linearRegCostFunction,
                       x0=theta,
                       args=(X, y, lambdaa),
                       method='TNC',
                       jac=linearRegGrad,
                       options={'disp': True})
    return res

def learningCurves(Xtrain,ytrain,Xval,yval,lambdaa):
    m = Xtrain.shape[0]
    errorTrain = np.zeros((m,1))
    errorCv = np.zeros((m,1))
    for i in range(1,m+1):
        optTheta = trainLinearReg(Xtrain[:i,],y[:i],lambdaa)['x']
        errorTrain[i-1] = linearRegCostFunction(optTheta,Xtrain[:i,],ytrain[:i],0)
        errorCv[i-1] = linearRegCostFunction(optTheta,Xval,yval,0)

    return errorTrain,errorCv

def randomLearningCurves(Xtrain,ytrain,Xval,yval,lambdaa):
    m = Xtrain.shape[0]
    randomErrorTrain = np.zeros((m,1))
    randomErrorCv = np.zeros((m,1))
    repeat = 50
    for r in range(repeat):
        for i in range(1,m+1):
            trainNum = i
            trainIndex = random.sample(range(0,m),trainNum)
            randomXtrain = Xtrain[trainIndex]
            randomYtrain = y[trainIndex]
            cvNum = i
            cvIndex = random.sample(range(0,m),cvNum)
            randomXcv = Xval[cvIndex]
            randomYcv = yval[cvIndex]
            # print(randomXtrain,randomYtrain)
            optTheta = trainLinearReg(randomXtrain,randomYtrain,lambdaa)['x']
            randomErrorTrain[i-1] = linearRegCostFunction(optTheta,randomXtrain,randomYtrain,0)
            randomErrorCv[i-1] = linearRegCostFunction(optTheta,randomXcv,randomYcv,0)
    randomErrorTrain = randomErrorTrain / repeat
    randomErrorCv = randomErrorCv/ repeat
    return randomErrorTrain,randomErrorCv

def normalizeFeature(df):
    return df.apply(lambda column: (column-column.mean())/column.std())


def  polyFeatures(x, power,as_ndarray=False):

    # construct dictionary and change it to dataFrame
    data = {'f{}'.format(i):np.power(x,i) for i in range(1,power+1)}
    df = pd.DataFrame(data)
    return df.to_numpy() if as_ndarray else df

def preparePloyData(*args,power):
    '''
    args: keep feeding in Xtrain, Xval, or Xtest will return in the same order
    '''
    def prepare(x):
        df = polyFeatures(x,power)
        ndarr = normalizeFeature(df).to_numpy()
        return np.insert(ndarr,0,np.ones(ndarr.shape[0]),axis=1)     
    
    return [prepare(x) for x in args]



X, y, Xval, yval, Xtest, ytest = loatData()
# print(X,y,Xval,yval,Xtest,ytest)
# plotData(X,y)
# print(y)
XtrainOne, XvalOne, XtestOne = [np.insert(x.reshape(x.shape[0], 1), 0, np.ones(x.shape[0]), axis=1) for x in (X, Xval, Xtest)]
XtrainPloy,XvalPloy,XtestPloy = preparePloyData(X,Xval,Xtest,power=8) 

# print(X)
theta = np.array([1,1])
lambdaa = 1
m = X.shape[0]
# J = linearRegCostFunction(theta,X,y,lambdaa)
# grad = linearRegGrad(theta,X,y,lambdaa)
# print(J,grad) # 303.9931922202643 [-15.30301567 598.25074417]


fg,ax = plt.subplots(3,4,figsize = (12,8))
ax = ax.flatten()


# data
ax[0].scatter(X,y,s=50,c='y',marker='o',label="Training data")
ax[0].set_xlabel('water_level')
ax[0].set_ylabel('flow')
ax[0].set_title('data')

optTheta = trainLinearReg(XtrainOne,y,0)['x']
# print(optTheta)
# underfit line
ax[1].scatter(X,y,s=50,c='y',marker='o',label="Training data")
ax[1].plot(X, X*optTheta[1] + optTheta[0] , label="Prediction")
ax[1].set_xlabel('water_level')
ax[1].set_ylabel('flow')
ax[1].legend(loc='best')
ax[1].set_title('underfit')


# underfit
errorTrain,errorCv = learningCurves(XtrainOne,y,XvalOne,yval,0)
ax[2].plot(np.arange(1,m+1),errorTrain,label='errorTrain')
ax[2].plot(np.arange(1,m+1),errorCv,label='errorCv')
ax[2].legend(loc='best')
ax[2].set_xlabel('m(training set size)')
ax[2].set_ylabel('error')
ax[2].set_title('underfit learning Curves')



# overfit data
optTheta = trainLinearReg(XtrainPloy,y,0)['x']
ax[3].scatter(X,y,c='y',marker='o',label="Training data")
XX = np.linspace(-50,50,100)
XXfit = preparePloyData(XX,power=8)[0]
yy =  XXfit @ optTheta
ax[3].plot(XX,yy,label='Prediction')
ax[3].set_xlabel('water_level')
ax[3].set_ylabel('flow')
ax[3].legend(loc='best')
ax[3].set_title('overfit')


#overfit
errorTrain,errorCv = learningCurves(XtrainPloy,y,XvalPloy,yval,0)
ax[4].plot(np.arange(1,m+1),errorTrain,label='errorTrainPloy')
ax[4].plot(np.arange(1,m+1),errorCv,label='errorCvPloy')
ax[4].legend(loc='best')
ax[4].set_xlabel('m(training set size)(lambda=0)')
ax[4].set_ylabel('error')
ax[4].set_title('overfit learning Curves')


# lambda= 1 learning curve
errorTrain,errorCv = learningCurves(XtrainPloy,y,XvalPloy,yval,1)
ax[5].plot(np.arange(1,m+1),errorTrain,label='errorTrainPloy')
ax[5].plot(np.arange(1,m+1),errorCv,label='errorCvPloy')
ax[5].legend(loc='best')
ax[5].set_xlabel('m(training set size)(lambda=1)')
ax[5].set_ylabel('error')
ax[5].set_title('lambda= 1 learning Curves')



# lambdaa = 1 fitting
optTheta = trainLinearReg(XtrainPloy,y,1)['x']
ax[6].scatter(X,y,c='y',marker='o',label="Training data")
XX = np.linspace(-50,50,100)
XXfit = preparePloyData(XX,power=8)[0]
yy =  XXfit @ optTheta
ax[6].plot(XX,yy,label='Prediction')
ax[6].set_xlabel('water_level(lambda=1)')
ax[6].set_ylabel('flow')
ax[6].legend(loc='best')
ax[6].set_title('lambda= 1 fit')


# lambdaa = 100 learning curve
errorTrain,errorCv = learningCurves(XtrainPloy,y,XvalPloy,yval,100)
ax[7].plot(np.arange(1,m+1),errorTrain,label='errorTrainPloy')
ax[7].plot(np.arange(1,m+1),errorCv,label='errorCvPloy')
ax[7].legend(loc='best')
ax[7].set_xlabel('m(training set size)(lambda=100)')
ax[7].set_ylabel('error')
ax[7].set_title('lambda= 100 learning Curves')


# lambdaa = 100 fit
optTheta = trainLinearReg(XtrainPloy,y,100)['x']
ax[8].scatter(X,y,c='y',marker='o',label="Training data")
XX = np.linspace(-50,50,100)
XXfit = preparePloyData(XX,power=8)[0]
yy =  XXfit @ optTheta
ax[8].plot(XX,yy,label='Prediction')
ax[8].set_xlabel('water_level(lambdaa = 100)')
ax[8].set_ylabel('flow')
ax[8].legend(loc='best')
ax[8].set_title('lambda= 100 fit')


lambdaa = 1
randomErrorTrain,randomErrorCv = randomLearningCurves(XtrainPloy,y,XvalPloy,yval,lambdaa)
ax[9].plot(np.arange(1,m+1),randomErrorTrain,label='errorTrainPloy')
ax[9].plot(np.arange(1,m+1),randomErrorCv,label='errorCvPloy')
ax[9].legend(loc='best')
ax[9].set_xlabel('random m(training set size)(lambda=1)')
ax[9].set_ylabel('error')
ax[9].set_title('lambda= 1 random')


lambdaaCandidate =[0,0.001,0.003,0.01,0.03,0.1,0.3,1,3,10]
errorT,errorC = [],[]
for l in lambdaaCandidate:
    optTheta = trainLinearReg(XtrainPloy,y,l)['x']
    errorT.append(linearRegCostFunction(optTheta,XtrainPloy,y,0))
    errorC.append(linearRegCostFunction(optTheta,XvalPloy,yval,0))

# print(lambdaaCandidate[np.argmin(errorC)]) = 1
# different lambda 
ax[10].plot(lambdaaCandidate,errorT,label='errorTrainPloy')
ax[10].plot(lambdaaCandidate,errorC,label='errorCvPloy')
ax[10].legend(loc='best')
ax[10].set_xlabel('lambda')
ax[10].set_ylabel('error')
ax[10].set_title('lambda and errorTrain errorCv')


errorTest = []
for l in lambdaaCandidate:
    optTheta = trainLinearReg(XtrainPloy,y,l)['x']
    errorTest.append(linearRegCostFunction(optTheta,XtestPloy,ytest,0))
print(lambdaaCandidate[np.argmin(errorTest)])
# 0.3
ax[11].plot(lambdaaCandidate,errorTest,label='errorTestPloy')
ax[11].legend(loc='best')
ax[11].set_xlabel('lambda')
ax[11].set_ylabel('errorTest')
ax[11].set_title('lambda and errorTest')


plt.tight_layout()
plt.show()