主要内容有:
- SVM相关知识点:cost function、最大间隔超平面、核函数
- python代码实现ex6的练习(包括画出支持向量和最大间隔超平面)
这篇博客的主要来源是吴恩达老师的机器学习第7周的学习课程,还有一些内容参考自黄海广博士的笔记GitHub
我先根据作业完成了matlab代码,并将它用python来实现(博客中无matlab实现)
实现过程中我结合吴恩达老师的上课内容和matlab代码修改了一部分代码(个人认为可以优化的地方)
SVM 相关知识点
Optimization Objective
我们先回顾下逻辑回归中的知识点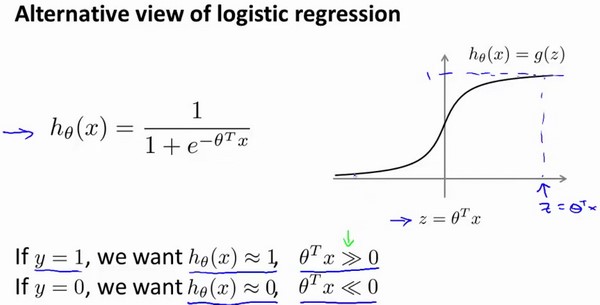
如上图所示
$\theta^{T}x \gg 0… h_{\theta}(x) \approx 1$
$\theta^{T}x \ll 0… h_{\theta}(x) \approx 0$
单样本的逻辑回归函数我们会这样表示: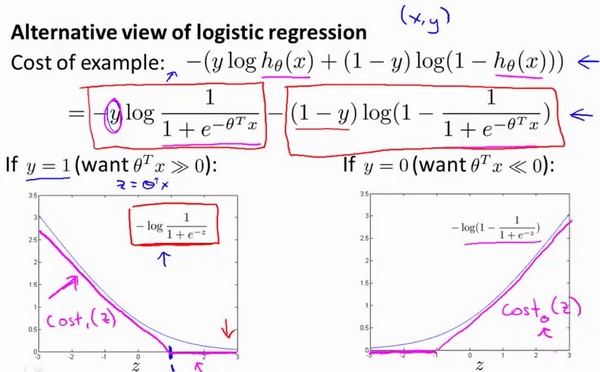
上图中的$y=1..y=0$的cost曲线是一条log函数曲线(蓝色),下面从逻辑回归的cost改进到SVM的cost function,SVM的单个样本的cost可以认为是上图中的紫红色曲线,它表示的是hinge loss
如上图所示:
- $y = 1时,z = \theta^{T}x \geq 1时,cost = 0 $
- $y = 0时,z = \theta^{T}x \leq -1时,cost = 0 $
这个叫做 Hinge Loss(合页损失函数),因为这个函数图像 像一本打开的书,所以就是合页了,怎么样理解SVM中的hinge-loss? - Slumbers的回答 - 知乎
下面是SVM的cost function定义: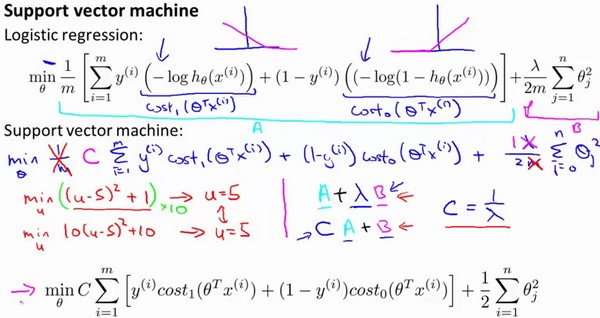
仔细查看上图(svm的正则化项下标应该是从$j=1$开始),我们可以看到,添加正则项的逻辑回归的代价函数是$A + \lambda \cdot B$的形式,我们如果给定$\lambda$,如果$\lambda$比较大时,就意味着B会有较大的权重
而SVM的优化目标函数为:
$min_{\theta} C\sum_{i=1}^{m}[y^{(i)}cost_{1}(\theta^{T}x^{(i)}) + (1-y^{i})cost_{0}(\theta^{T}x^{(i)}] + \frac{1}{2} \sum_{j=1}^{n} \theta_{j}^{2}$
相当于$C \cdot A + B$
如果我们让C非常小的话,同样也会给B较大的权重
从理解上来看,可以看成$C = \frac{1}{\lambda}$
这样的话,也就是把$A + \lambda \cdot B$ 除以 $\lambda$
变成了:
$C = \frac{1}{\lambda}$
虽然这两个表达式不同,但是当$C = \frac{1}{\lambda}$时,优化目标应该会得到相同的目标值,有相同的最优$\theta$
还有一个注意点是: SVM的优化目标相比较逻辑回归的少了除以$\frac{1}{m}$,由于$\frac{1}{m}$是一个常数,在最小化问题中,不论有没有这一项,得到的$\theta$应该是没有区别的(和除以$\lambda$相似。
最后是关于SVM的$h_{\theta}(x)$它不像逻辑回归一样得到的是概率值
SVM的假设函数是这样的:
$h_{\theta}(x) = \left\{\begin{matrix}
1 \quad if \ \theta^{T}x \geq 0
\\
0 \quad otherwise
\end{matrix}\right.
$
Large Margin Intuition
再次给出SVM的cost定义:
特别注意的是:
$\theta^{T} \geq 1 \quad \theta^{T} \leq -1$与逻辑回归中 $\theta^{T} \geq 0 \quad \theta^{T} \leq 0$ 的区别
相比较逻辑回归,SVM的要求更高:
- 只有$\theta^{T}x \geq 1$,我们的$y=1$的样本cost才会为0
- 只有$\theta^{T}x \leq -1$,我们的$y=0$的样本cost才会为0
相当于给SVM加入了一个safety margin factor
下面我们考虑当C设置的非常大时,我们会得到什么结果?
当C非常大时,要最小化代价函数,我们会希望
$min_{\theta} C\sum_{i=1}^{m}[y^{(i)}cost_{1}(\theta^{T}x^{(i)}) + (1-y^{i})cost_{0}(\theta^{T}x^{(i)}] + \frac{1}{2} \sum_{j=1}^{n} \theta_{j}^{2}$
有最优解,那么我们会尽量让代价函数的第一项为0
那么我们就需要找到一个$\theta$
使得 $\theta^{T}x \geq 1 \quad(y=1)$
或者
$\theta^{T}x \leq -1 \quad(y=0)$
有了这两个约束条件,当我们最小化$\theta$时,我们就会得到一个非常有趣的决策边界
上图中紫红色、绿色、黑色都可以是边界,显然黑色的边界是最好的,因为它使得分类具有更强的鲁棒性,当我们加入一个样本时,如果在黑色边界下方一点点,我们的SVM可能依旧能够正确分类,但是如果我们的样本是紫红色或者是绿色,很可能就不能正确分类了
SVM在求解优化问题后,会选择黑色决策面作为我们的分类决策面,它试图找到一个最大间隔(margin),用来作为决策平面,但是SVM是如何找到这个最大间隔超平面呢? 在下一小节吴恩达老师给了intuition
下面讨论C对决策面的影响: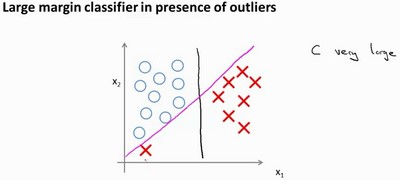
在没有左下角红色的样本时,我们的SVM可能得到了黑色的决策面,但是如果我们加入了左下角红色样本(outlier,异常点),如果我们将C设置的非常大,我们的SVM就可能得到了粉色的决策面,这将是非常不明智的选择,但是如果C设置的小一些,我们就可能会得到黑色的决策面,也就是说,C取值合理时,SVM会忽略掉样本的一些outliers,并做出合理的决策(即使数据是非线性可分)
至于C的取值为什么会造成这样的影响,我们可以这样理解:
C可以认为是$C = \frac{1}{\lambda}$,我们在学习逻辑回归的时候知道,当$\lambda$非常大时,容易造成欠拟合,当$\lambda$非常小时,容易造成过拟合,所以C非常大时,即可以认为$\lambda$非常小,它会导致过拟合,也就是SVM的分类器试图将全部样本分类正确,也就导致了决策面变为了粉色的那条
Mathematics Behind Large Margin Classification
首先我们需要知道一个向量$\vec{v}$在向量$\vec{u}$方向上面的投影的计算:
$P = \parallel \vec{v} \parallel \cdot cos(\theta)$
$= \parallel \vec{v} \parallel \cdot \frac{\vec{u}^T \cdot \vec{v} }{\parallel\vec{v} \parallel \cdot \parallel\vec{u} \parallel} $
$= \frac{\vec{u}^T \cdot \vec{v}}{ \parallel\vec{u} \parallel} $
因为余弦值可能是负的,所以投影也可能是负的
下面讨论svm的优化目标(这里省略了svm优化目标的第一项),并且为了简化只是设置我们的数据特征$n=2$的时候,并且$\theta_{0}=0$
下图给出了我们的$\theta^{T}x^{(i)}$是如何计算的: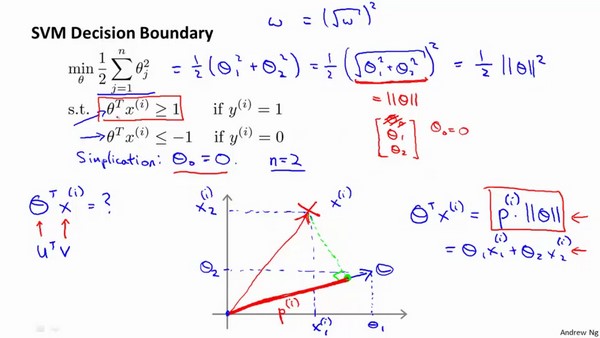
由上图我们可以知道:
$\theta^{T}x^{(i)} = P^{(i)} \cdot \parallel \theta \parallel = \theta_{1}x_{1}^{(i)} + \theta_{2}x_{2}^{(i)}$
这里告诉我们:
$\theta^{T}x^{(i)} \geq 1$是可以用 $P^{(i)} \cdot \parallel \theta \parallel \geq 1$替代的
同理:
$\theta^{T}x^{(i)} \leq -1$是可以用 $P^{(i)} \cdot \parallel \theta \parallel \leq -1$替代的
更改约束条件之后,我们可以看看SVM会选择什么的超平面
实际上由于数学知识,我们可以知道:$\theta$是我们决策面的法向量,$\theta_{0}=0$意味着我们的决策面是通过原点的
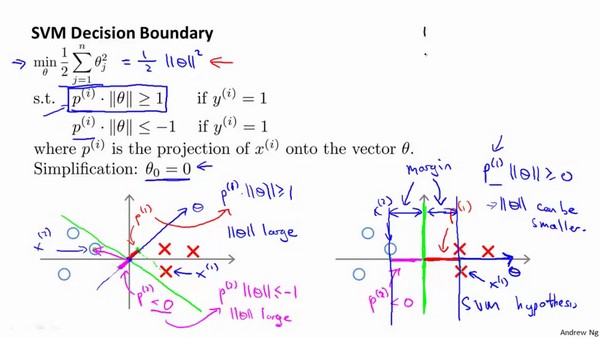
上图解释了为什么SVM决策时得到的超平面是上图右边,而不是上图左边的超平面
对于每个$x^{(i)}$,我们有$p^{(i)} \cdot \parallel \theta \parallel \geq 1 or \leq -1$
如果$p^{(i)}$很小的话,我们$\parallel \theta \parallel$就会变得非常大(投影为负就是$\leq -1$的时候,同样要求$\parallel \theta \parallel$非常大),而我们的优化目标是要让$\parallel \theta \parallel$变得非常小,所以,SVM会尽可能的选择大间隔超平面,它会使得$p^{(1)},p^{(2)},p^{(3)}$越大,最终我们的$\parallel \theta \parallel$会越小
注意我们化简后目标是使得
$min_{\theta} \ \frac{1}{2} \sum_{j=1}^{n} \theta_{j}^{2}$
$=\frac{1}{2} \parallel \theta \parallel ^2$
最小,所以当我们选择大间隔时,我们在让:
$max \ p^{(i)}$
$p^{(i)}$是训练样本到我们的决策面的距离
这样,我们会使得$\parallel \theta \parallel$越小,我们的优化目标也会越小
当然,即使$\theta_{0} \neq 0$时,证明也是类似的,它是上述情形的推广,SVM依旧可以找到最大间隔
下面是SVM核函数的内容,它使得SVM能够解决线性不可分的问题
Kernels
前面我们利用逻辑回归解决线性不可分问题时,我们一般会添加多项式特征(如进行原有特征的组合)
如下图所示:
但是如果我们输入的是图片的话,图片中有许多的像素点,那么我们构造上面的多项式特征计算代价就会非常大,下面看看SVM会如何解决

像上图一样,SVM通过landmark来构造新的特征,对于给定的样本$x$,它计算$f_{1} \ f_{2} \ f_{3}$来表示$x$与$l_{1} \ l_{2} \ l_{3}$的相似度
具体的计算就使用到了核函数,这里使用的是高斯核函数来计算,如下图所示:

通过使用landmark和similarity function定义新的特征$f_{0}= 1,\ f_{1} \ f_{2} \ f_{3}…f_{..}$,
我们就可以这样来预测样本:

可以看到 在红色曲线内部,SVM计算$\theta^{T}x > 0$,所以预测为1,在线外的预测为0,这样的话就会构成一个决策平面
至于高斯函数的图像可以参考下图: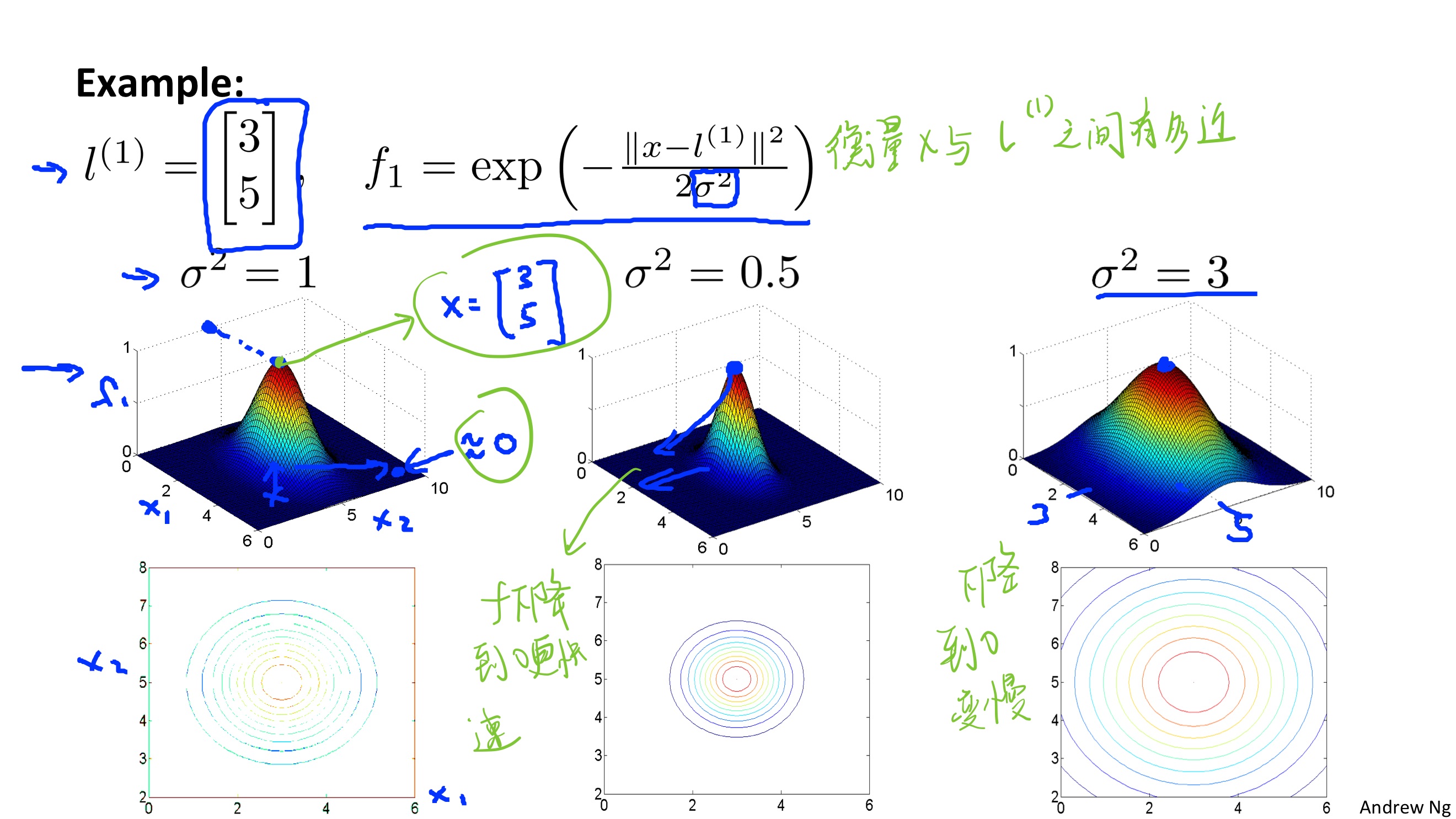
接下来我们还有一个问题,就是:如何选择landmark呢?
通常我们会将训练数据中的所有样本作为landmark,也就是说,如果我们有m发个样本,那么我们就有m个landmark,这样的话对于每个$x$,我们会有$m+1$个特征(1是$\theta_{0}$与它相乘),当然,其中必定有一个特征是为1,因为自己与自己的距离,通过高斯函数计算后为1,如下图所示:

将核函数运用到SVM中,我们可以得到下图:

这就是SVM的核心思想了,实际上在具体实现的时候,我们不最小化
$\parallel \theta \parallel^{2}$
而是选择优化
$\theta^{T} M \theta$
这样可以让SVM运行的更加高效,能让SVM适应更大的训练集,当然这只是实现上面的优化,本质上对于理解SVM是没有差别的,只是为了计算更加高效。
实际上不能把kernel实现运用到逻辑回归里面也是同样的问题,SVM具有很多的kernel tricks和computational tricks,它只能使用在SVM中,而不能用到其他算法上面,如果用在逻辑回归上面,那么计算也会相当的慢
SVM parameters
SVM中C和$\sigma^2$的选择技巧:

- C较大时,相当于λ较小,可能会导致过拟合,高方差
- C较小时,相当于λ较大,可能会导致低拟合,高偏差
- $\sigma^2$较大时,可能会导致低方差,高偏差
- $\sigma^2$较小时,可能会导致低偏差,高方差
对于$\sigma^2$的变化理解:
当$\sigma^2$越大时,我们的特征$f_{i}$变化的将会更加平滑,那么随着x的变化,我们得到的$\theta^{T}f$变化也会更加的平滑,方差也会变得更小
Using An SVM
强烈不建议自己实现SVM
但是使用libsvm软件库的时候,我们需要明确:
- 如何选择参数C
- 如何选择核函数(相似度函数)
比较常用的核函数:
linear kernel(No kernel)
等价于没有使用核函数,直接计算$\theta^{T}x \geq 0 \quad y=1$
它适用于n较大,但是m比较小的情况(没有足够的数据让我们训练一个复杂的模型,我们就可以选择逻辑回归或者不带核函数的(也就是线性核函数)的SVM)Gaussian kernel
高斯核函数需要我们去选择$\sigma^2$的取值,适用于n比较小,但是m比较大的情况
同时还需要注意:
在使用高斯核函数之前,需要特征归一化,以避免某个特征数值太大,让这个特征决定了我们相似性函数的取值,而使得其他特征不起作用
所有的核函数都需要满足”Mercer’s Theorem”,还有其他核函数用的比较少,这里不做总结了
SVM的多分类问题和逻辑回归是一样的,同样不做总结
logistic regression vs SVM
相对于m而言,n比较大的时候,训练集数据量不够支持我们训练一个复杂的非线性模型,我们选用逻辑回归模型或者不带核函数的支持向量机。(如n=10000,m=10~10000)
n较小,m大小中等,如n=1~1000,m=10~10000or50000,使用高斯核函数的支持向量机。
n较小,m较大,如n=1-1000,m>50000,则使用支持向量机(高斯核函数)会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向量机。
神经网络对于以上三种情况都可以表现的很好,但是神经网络会陷入局部最小值问题,梯度消失问题(虽然这些也不是大问题),而SVM,可以证明,它的cost function是convex函数,有全局最小值
最后的最后:
使用哪个算法实现其实没有关系
关键在于:
- 拥有多少的数据
- 特征的选取处理
- 有能力做好错类(误差)分析
- 在算法表现不好时能够找到优化方法(考虑、构造新的特征来获得更好的表现性能
至此,吴恩达老师监督学习算法内容已经结束了,下面几周的内容将会是是聚类、PCA等无监督学习的算法
代码实现
sklearn的使用:
1
2
3from sklearn import svm
from sklearn import metrics
from sklearn.linear_model import LogisticRegression导入data1,使用线性SVM进行分类,设置C=1和C=100,画出最大间隔超平面和支持向量(C=1,C=100)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16svc1 = svm.SVC(kernel='linear', C=1)
svc1.fit(data1[['X1','X2']],data1['y'])
# ss1 = svc1.score(data1[['X1','X2']],data1['y'])
xlim = ax[0].get_xlim()
ylim = ax[0].get_ylim()
xx = np.linspace(xlim[0], xlim[1], 50)
yy = np.linspace(ylim[0], ylim[1], 50)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = svc1.decision_function(xy).reshape(XX.shape)
ax[1].scatter(positive['X1'],positive['X2'],s=30,marker='o',c = 'r',label='Postive')
ax[1].scatter(negative['X1'], negative['X2'], s=30, marker='o',c='b' ,label='Negative')
ax[1].contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,linestyles=['--', '-', '--'])
ax[1].scatter(svc1.support_vectors_[:, 0], svc1.support_vectors_[:, 1], s=50,c='y',linewidth=1, facecolors='none', edgecolors='k')
ax[1].set_title('data1:dicesion boundary(C = 1)')实现效果图如下:
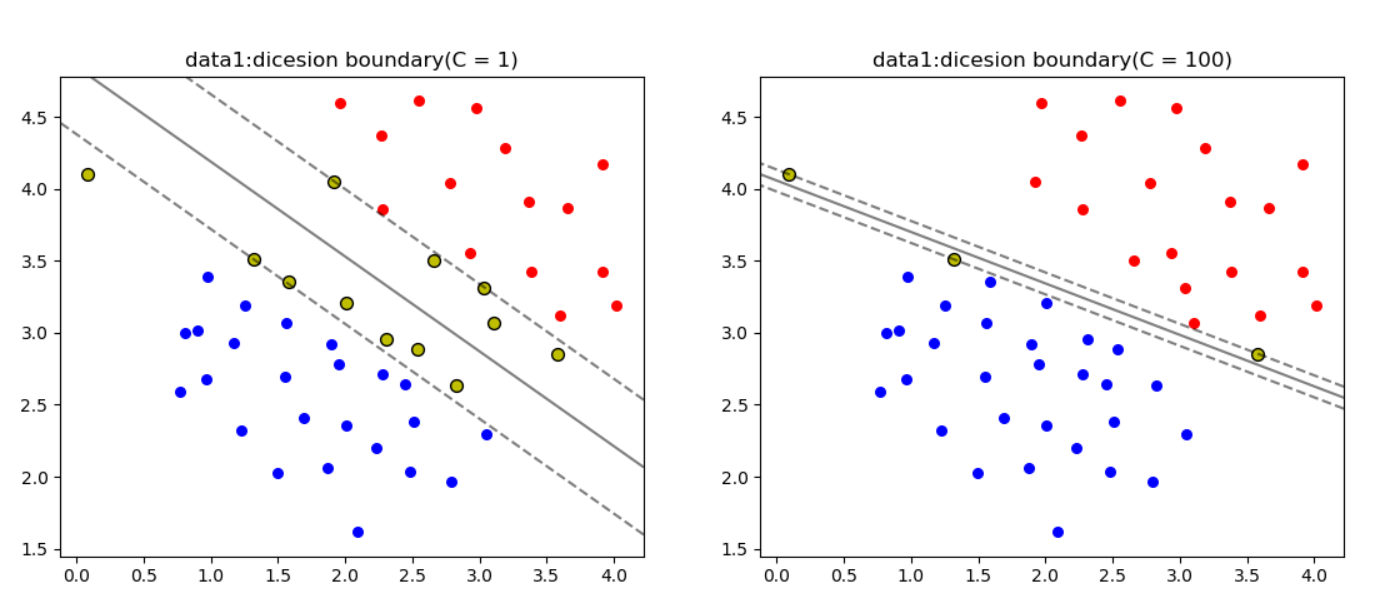
注:黄色的是支持向量导入非线性数据data2并且画出最大间隔超平面和支持向量
实现效果图如下: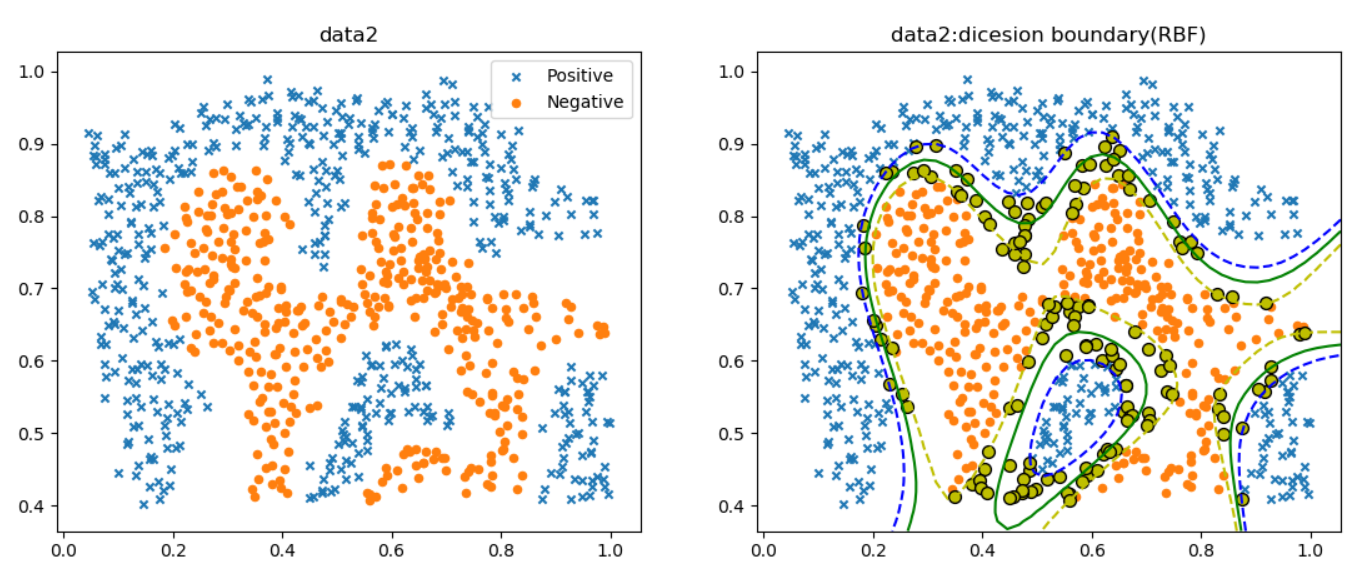
注:黄色的是支持向量导入data3,并训练最优参数C和$\sigma^2$,并画出最大间隔超平面和支持向量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
rawData3 = loadmat('data/ex6data3.mat')
X = rawData3['X']
Xval = rawData3['Xval']
y = rawData3['y'].ravel()
yval = rawData3['yval'].ravel()
C_Values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
gammaValues = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
bestScore = 0
bestParams = {'C': None, 'gamma': None}
for C in C_Values:
for gamma in gammaValues:
svc = svm.SVC(C=C, gamma=gamma)
svc.fit(X, y)
score = svc.score(Xval, yval)
if score > bestScore:
bestScore = score
bestParams['C'] = C
bestParams['gamma'] = gamma
# print(bestScore,bestParams)
最佳的C和$\sigma^2$值为:1
{'C': 0.3, 'gamma': 100}
画出的最大间隔超平面和支持向量如下(注:黄色的是支持向量)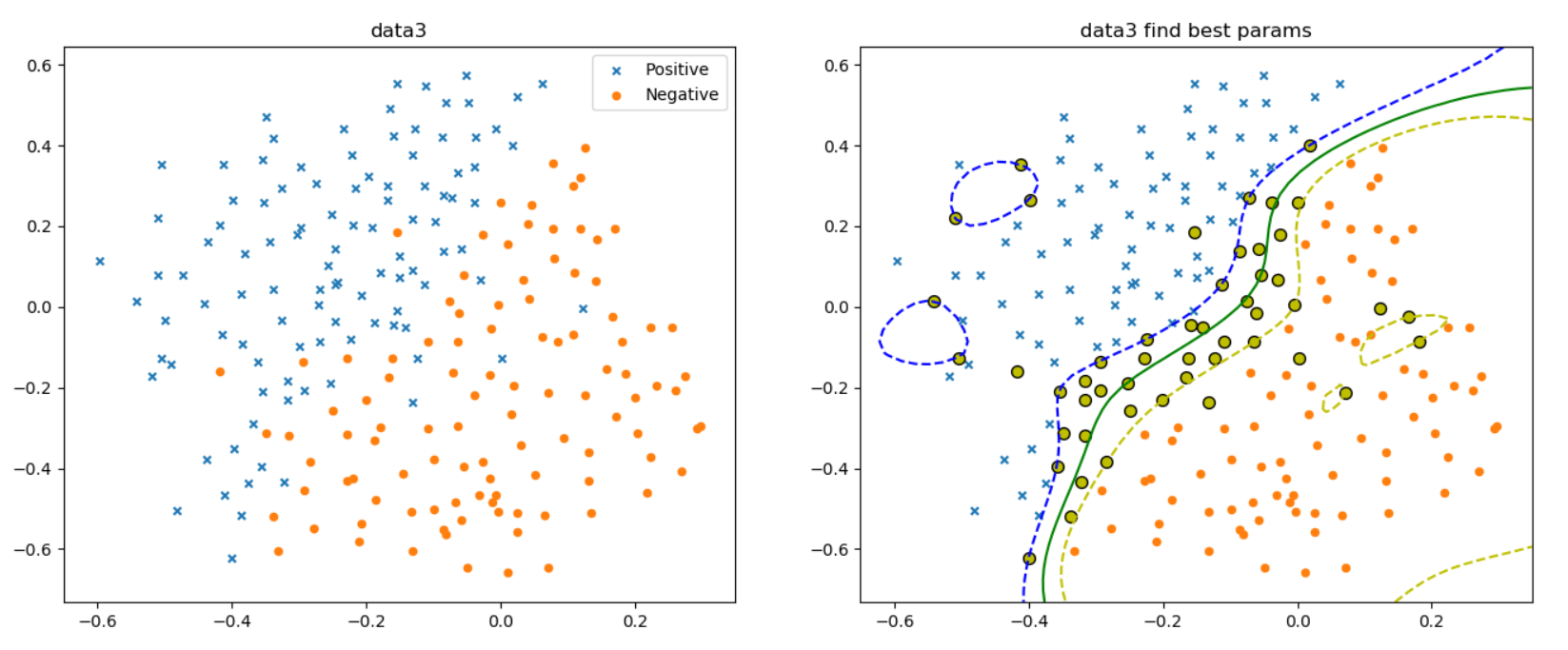
- 使用ex中给出的数据集进行垃圾邮件分类
首先给出的是SVM线性核函数的混淆矩阵,接着是使用高斯核函数的混淆矩阵,最后是逻辑回归的混淆矩阵可以看到,逻辑回顾和线性SVM表现的比高斯SVM要好1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30linear:
precision recall f1-score support
0 0.99 0.98 0.98 692
1 0.96 0.97 0.96 308
micro avg 0.98 0.98 0.98 1000
macro avg 0.97 0.98 0.97 1000
weighted avg 0.98 0.98 0.98 1000
rbf:
precision recall f1-score support
0 0.94 0.99 0.97 692
1 0.98 0.87 0.92 308
micro avg 0.95 0.95 0.95 1000
macro avg 0.96 0.93 0.94 1000
weighted avg 0.95 0.95 0.95 1000
LogisticRegression:
precision recall f1-score support
0 1.00 0.99 1.00 692
1 0.99 0.99 0.99 308
micro avg 0.99 0.99 0.99 1000
macro avg 0.99 0.99 0.99 1000
weighted avg 0.99 0.99 0.99 1000
完整代码将在本文最后给出。
- 相关注意点
- C parameter is a positive value that controls the penalty for misclassiffed training examples.
- A large parameter C tells the SVM to try to classify all the examples correctly. plays a role similar to , where is the regularization parameter that we were using previously for logistic regression
- Most SVM software packages (including svmTrain.m) automatically add the extra feature for you and automatically take care of learning the intercept term . So when passing your training data to the SVM software, there is no need to add this extra feature yourself.
To find nonlinear decision boundaries with the SVM, we need to first implement a Gaussian kernel. You can think of the Gaussian kernel as a similarity function that measures the ‘distance’ between a pair of examples, . The Gaussian kernel is also parameterized by a bandwidth parameter, , which determines how fast the similarity metric decreases (to 0) as the examples are further apart.
One method often employed in processing emails is to ‘normalize’ these values, so that all URLs are treated the same, all numbers are treated the same, etc. For example, we could replace each URL in the email with the unique string “httpaddr” to indicate that a URL was present. This has the effect of letting the spam classifier make a classification decision based on whether any URL was present, rather than whether a specific URL was present
This typically improves the performance of a spam classifier, since spammers often randomize the URLs, and thus the odds of seeing any particular URL again in a new piece of spam is very small.
References
完整代码
1 | import numpy as np |